Научный журнал

Вестник Алтайской академии экономики и права

Print ISSN 1818-4057

Online ISSN 2226-3977

Перечень ВАК

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Огорелкова Н.В. 1 Реутова И.М. 2 Свердлина Е.Б. 1

---

1 ОмГУ им. Ф.М. Достоевского

2 СЗИУ РАНХиГС

Исследование посвящено рассмотрению и анализу подходов к критериям оценки эффективности управления инвестиционных портфелей негосударственных пенсионных фондов при размещении средств пенсионных резервов. В статье анализируются достоинства и недостатки показателей, используемых для оценки и анализа эффективности управления пенсионными резервами/накоплениями: Шарпа, Трейнора, Альфа Дженсена, коэффициента Модильяни, Сортино, Штуцера, Омеги, а также модифицированного коэффициента Шарпа. Непосредственно анализ эффективности управления портфелями пенсионных резервов проводился на основе статистических данных по 31 НПФ за 2016–2020 гг. Были сделаны выводы о необходимости включения в методики оценки эффективности управления портфелями расчет коэффициентов Шарпа и Альфа Дженсена. Для осуществления дополнительного анализа, осуществления внутригрупповых и межгрупповых сравнений, формирования дополнительных критериев при формировании ренкингов НПФ и их управляющих компаний рекомендовано использовать коэффициенты Модильяни и Трейнора. Кроме того, желательно использование квартальных оценок доходности, но из-за малого количества наблюдений, использование модифицированного коэффициента Шарпа не целесообразно, поскольку это будет влиять на искажение итоговых данных.

Статья в формате PDF

438 KB

пенсионные накопления

пенсионные резервы

негосударственные пенсионные фонды

управляющие компании

эффективность управления инвестиционными портфелями

1. Абрамов А.Е., Радыгин А.Д., Чернова М.И. Эффективность управления портфелями паевых инвестиционных фондов акций и ее оценка // Экономическая политика. 2019. № 4. С. 8-47.

2. Абрамов А.Е., Чернова М.И. Анализ эффективности портфелей негосударственных пенсионных фондов и паевых инвестиционных фондов в Российской Федерации // Глобальные рынки и финансовый инжиниринг. 2015. № 1. С. 15–40.

3. Берзон Н.И., Дорошин Д.И. Особенности применения показателей эффективности финансовых инвестиций // Финансы и кредит. 2012. № 14(494). С. 21–33.

4. Болдырева Н.Б., Решетникова Л.Г. Об эффективности инвестиционной деятельности управляющих в системе обязательного пенсионного страхования // Вестник Санкт-Петербургского университета. Экономика. 2020. № 3. С. 483-513.

5. Буренин А.Н. Управление портфелем ценных бумаг. М.: НТО им. Академика С.И. Вавилова, 2008. 440 с.

6. Ногин Ю.Б. Анализ эффективности управления средствами пенсионных накоплений и пенсионных резервов российскими негосударственными пенсионными фондами // Корпоративные финансы. 2017. № 1. С. 100-110.

7. Решетникова Л.Г. Эффективность участия негосударственных пенсионных фондов в системе инвестирования средств пенсионных накоплений // Вестник ОмГУ. Серия: Экономика. 2011. №1. С. 44-48.

8. Туманянц К.А., Тимофеева Г.В., Тимофеев Ю.В. Влияние эффективности инвестирования на конкурентность пенсионного рынка России // Вестник НГУЭУ. 2015. №3. С. 39-55.

9. Фатхлисламова Г.Ф. Исследование результатов инвестирования средств пенсионных накоплений // Управление. 2018. № 4 (22). С.40-46.

10. Федорова Е.А. Сырцев В.А. Оценка эффективности деятельности компаний, управляющих пенсионными накоплениями на основе модели Кобба-Дугласа // Экономический анализ: теория и практика. 2014. № 18. С. 33-39.

11. Основные показатели деятельности негосударственных пенсионных фондов. Банк России. URL:https://www.cbr.ru/finmarket/supervision/sv_coll/ops_npf/ (дата обращения: 12.05.2021).

12. Национальное рейтинговое агентство. Методология присвоения некредитных рейтингов надежности и качества услуг негосударственным пенсионным фондам по национальной шкале негосударственных пенсионных фондов для Российской Федерации.

13. РАЭксперт, Методология присвоения рейтингов финансовой надежности НПФ URL: https://www.raexpert.ru/docbank//f90/264/d26/f1a992c782bf6d81920d71c.pdf.

14. Рейтинговое агентство АКРА (Методология присвоения кредитных рейтингов НПФ по национальной шкале для Российской Федерации). URL: https://acra-ratings.ru/upload/iblock/a2f/anrimp4dij4hdhlearwlbz9dt3nsq04d/20211203_ACRA_NSPF.pdf.

15. Sharpe W.F. The Sharpe ratio. Journal of Portfolio Management. 1994. № 2.

16. Treynor J.L., Black F. How to use security analysis to improve portfolio selection. Journal of Business. 1973. № 1.

17. Jensen M. The Performance of mutual funds in the period 1945-1964. Journal of Finance. 1968. № 23.

18. Modigliani F and Modigliani L. Risk- adjusted performance: how to measure it and why. Journal of Portfolio Management. 1997. № 23.

19. Sortino F., Price L. Performance Measurement in a Downside Risk Framework. Journal of Investing. 1994.

20. Pezier J., White A. The relative Merits of Investable Hedge Fund indices and of Funds of Hedge Funds in Optimal Passive Portfolios. 2006. URL: https://ideas.repec.org/p/rdg/icmadp/icma-dp2006-10.html (дата обращения: 04.12.2021).

21. Keating C., Shadwick W.F. A Universal Performance Measure. The Finance Development Center. May, 2002.

Введение

Оценка эффективности управления инвестиционными портфелями осуществляется согласно теории портфельного инвестирования на основе коэффициентов Шарпа [15], Трейнора [16], Альфа Дженсена [17], Модильяни [18], Сортино [19], Штуцера, Омеги [21], модифицированного коэффициента Шарпа [20] и ряда других. Обзор литературы и особенностей использования данных коэффициентов описаны А.Н. Бурениным [5], анализ особенностей применения данных коэффициентов на различных временных горизонтах, ограничения при их использовании для акций и облигаций на российском рынке осуществлены в работе Н.И. Берзона и Д.И. Дорошина [3].

Следует напомнить, что инвестиционная деятельность негосударственных пенсионных фондов (НПФ) имеет свою специфику, кроме того, возможность расчета тех или иных показателей связаны с наличием или отсутствием соответствующей статистики. НПФ не являются организациями, осуществляющими публичное размещение и обращение ценных бумаг, и, соответственно, не имеют биржевых котировок. Поэтому не все показатели могут быть использованы в качестве критерия эффективности управления портфелями НПФ.

Несмотря на наличие обширной литературы по исследованию пенсионной системы РФ, аспекты, связанные с анализом эффективности управления портфелей пенсионных резервов/накоплений НПФ, изучены недостаточно. Нет единого мнения о показателях, которые могли бы выступать в качестве критерием эффективности портфелей. Чаще всего в литературе используются показатели доходности НПФ, как валовой (доходность до выплаты вознаграждения управляющим компаниям, специализированному депозитарию и фонду), так и «чистой» (доходность за минусом вознаграждения управляющим компаниям, специализированному депозитарию и фонду). В статье Г.Ф. Фатхслисламовой при анализе эффективности инвестирования пенсионных накоплений наряду с показателями доходности рекомендует использовать показатели накопленных убытков и накопленной убыточности [9].

Необходимо отметить, что показатели доходности от размещения пенсионных резервов/инвестирования пенсионных накоплений используются для оценки эффективности управления пенсионными резервами/пенсионными накоплениями двумя рейтинговыми агентствами: РАЭксперт (Методология присвоения рейтингов финансовой надежности негосударственным пенсионным фондам [РАЭксперт]) и Национальным рейтинговым агентством, (Методология присвоения некредитных рейтингов надежности и качества услуг негосударственным пенсионным фондам по национальной шкале негосударственных пенсионных фондов для Российской Федерации [НРА]). Согласно данным методикам, накопленная доходность, рассчитываемая по формуле И. Фишера, за последние три года. Оценка осуществляется в сравнении со среднеотраслевыми показателями.

Показатель доходности в соотношении с риском портфеля как критерий эффективности используется в работах Абрамова А.Е., Радыгина А.Д., Черновой М.И. [1; 2]. В качестве критерия эффективности портфеля пенсионных накоплений/пенсионных резервов наряду с доходностью применяется коэффициент Шарпа в статьях [7], [8], [4]. В работе Ю.Б. Ногина для оценки результативности управления пенсионными накоплениям/резервами НПФ предложено использовать коэффициенты Шарпа и Альфа Дженсена [6].

Аналогичный подход применяет Рейтинговое агентство АКРА (Методология присвоения кредитных рейтингов негосударственным пенсионным фондам по национальной шкале для Российской Федерации [14]. Согласно данной методике, результаты инвестирования НПФ определяются на основе соотношения двух коэффициентов, учитывающих риск и доходность инвестиций: коэффициента Шарпа и коэффициента Альфы Дженсена. Период расчета – 5 лет. Рассчитанные коэффициенты сравниваются со среднеотраслевыми значениями, в зависимости от соотношения полученных показателей присваиваются рейтинговые баллы.

Цель данной работы – проанализировать возможность использования дополнительных показателей для оценки эффективности управления пенсионными накоплениями/резервами НПФ накоплений путем построения эконометрических моделей и на этой основе выбор аналитического инструментария исследования.

Материалы и методы исследования

В качестве объектов исследования использованы данные по 31 НПФ, осуществляющему на конец 2020 г. деятельность по негосударственному пенсионному обеспечению.

Результаты исследования и их обсуждение

Рассмотрим особенности показателей, используемых для оценки и анализа эффективности управления пенсионными резервами/накоплениями.

Коэффициент Шарпа является наиболее известным показателем эффективности портфельного инвестирования и рассчитывается в отношении НПФ по следующей формуле:

Shi = (Ri – Rm ) / σi

где Shi – коэффициент Шарпа i-ого НПФ;

Ri – накопленная доходность инвестирования портфеля пенсионных накоплений (резервов) i-ого НПФ за последние завершившиеся пять календарных лет, рассчитанная по формуле Ирвина-Фишера;

Rm – накопленная доходность рынка пенсионных накоплений (пенсионных резервов) за последние завершившиеся пять календарных лет, рассчитанная по формуле Ирвина-Фишера;

σi – историческая волатильность доходности инвестирования портфеля пенсионных накоплений (резервов) i-ого НПФ за последние завершившиеся пять календарных лет [9, С. 103]

В отношении НПФ коэффициент Шарпа можно интерпретировать следующим образом: коэффициент Шарпа позволяет дать ответ, насколько успешной была принятая инвестиционная стратегия НПФ и обогнала ли она среднюю рыночную доходность. Коэффициент Шарпа показывает, какую дополнительную доходность выше среднерыночной приносит портфель пенсионных накоплений/резервов НПФ на единицу совокупного риска портфеля, измеряемую стандартным отклонением. К недостаткам данного коэффициента можно отнести:

− его значительную чувствительность к отдельным параметрам, – так если волатильность портфеля будет низкой и будет стремиться к нулю, то значение коэффициента Шарпа будет чрезмерно завышено и не будет отражать истинную эффективность портфеля;

− коэффициента Шарпа отражает совокупный риск портфеля, как систематический, рыночный, так и несистематический [3, С.23].

Данная проблема решается при расчете коэффициента Трейнора, который в отношении НПФ будет рассчитываться как превышение доходности портфеля пенсионных накоплений/резервов конкретного НПФ над среднерыночной доходностью рынка пенсионных накоплений/резервов, деленное на рыночный риск портфеля накоплений/резервов данного НПФ, определяемого коэффициентом, бета портфеля.

Тi = (Ri – Rm ) / βi

где β i – бета-коэффициент портфеля пенсионных накоплений i-ого НПФ.

Более высокое значение коэффициента Трейнора показывает, какой портфель пенсионных накоплений/резервов НПФ будет более диверсифицированным. Коэффициент Трейнора отражает превышение доходности портфеля пенсионных накоплений (резервов) НПФ над среднерыночной доходностью только в отношении рыночного риска, тогда как коэффициент Шарпа отражает превышение доходности портфеля пенсионных накоплений (резервов) НПФ над среднерыночной доходностью в отношении всего риска портфелей.

Еще один недостаток коэффициента Шарпа – учет как положительного, так и отрицательного изменения доходности, тогда как инвесторы более чувствительны к падению доходности, корректируется коэффициентом Сортино. В коэффициенте Сортино используется показатель полудисперсии, при расчете которого используются только по отрицательные отклонения доходности. Коэффициенте Сортино оценивает только риск снижения доходности портфеля, что позволяет получить дополнительную оценку эффективности портфеля. Однако, некоторые недостатки данного подхода не позволяют использовать его для оценки эффективности управления портфелями НПФ. Коэффициент Сортино рекомендуют использовать на максимально длинных временных рядах. Так как нет ежедневных котировок и рыночной оценки портфеля НПФ, то сформировать значительные временные ряды статистических данных для НПФ практически невозможно. Кроме того, на длительном временном промежутке инвестирования НПФ дают положительную доходность, поэтому становится невозможным рассчитать как полудисперсию по отрицательным отклонениям, так и коэффициент Сортино.

Следующий показатель – коэффициент Альфа Дженсена используется для количественной оценки эффективности деятельности управляющих инвестиционными фондами. Показатель Альфа позволяет оценить дополнительную доходность, полученную благодаря выбору изначально недооцененного актива [18]. В отношении НПФ данный коэффициент может быть использован для оценки эффективности управления портфелем пенсионных накоплений(резервов) и позволяет дать ответ, насколько эффективно была реализована разработанная инвестиционная стратегия НПФ, сравнить результаты инвестирования пенсионных накоплений/резервов НПФ с заданными «бенчмарками» и определить в какой степени управляющий обыгрывает рынок или проигрывает рынку.

Коэффициент Альфа Дженсена рассчитывается как разница между фактической и расчетной (математически оптимальной) доходностью пенсионных средств НПФ [6, C. 103] по формуле:

ai = Ri – (Rf + βi * [Rm – Rf])

где ai – коэффициент альфа Дженсена;

Rf – доходность безрисковой ставки или альтернативного вложения;

βi – бета-коэффициент портфеля пенсионных накоплений (резервов) i-ого НПФ.

Коэффициент Модильяни основывается на совокупном риске финансового актива, рассчитывается по следующей формуле:

M2 = (Ri – Rf )* (σm / σi) + Rf

где σi и σm – стандартные отклонения доходностей портфеля и рынка, соответственно.

Коэффициент Модильяни определяет премию за риск для портфеля, созданного на основе оцениваемого портфеля, риск которого равен риску рыночного портфеля [18, С 376]. В отношении НПФ показывает какая доходность была бы получена, если бы совокупный риск портфеля был равен рыночному риску, т. е. удалось ли сформировать из средств пенсионных накоплених/резервов широко диверсифицированный портфель.

Так как при расчете коэффициента Шарпа используется предположение о нормальном распределении доходности J.Pezier и А.White предложили использовать модифицированный коэффициент Шарпа [20]. При его расчете коэффициент Шарпа корректируется на показатели – коэффициент асимметрии и коэффициенте эксцесса:

Shm = Sh * [1 + Sh * As / 6 – Sh2* Ek \ 24]

где Sh – коэффициент Шарпа;

As – коэффициент асимметрии показывает степень несимметричности числовых данный относительно среднего значения;

Ek – коэффициент эксцесса, мера остроты пика распределения случайной величины

Показатель Омега, предложенный в 2002 г. С.Keating и W.F.Shadwick, считается более комплексным показателем по сравнению в коэффициенты Шарпа, Трейнора, Дженсена или Сортино, позволяющим сравнивать портфели с распределением доходности, отличным от нормального. При его расчете оценка портфеля осуществляется относительно минимально допустимого и установленного инвестором порога доходности. Омега показывает, насколько превышена эта минимальная доходность [21].

Для целей всестороннего анализа различных аспектов эффективности инвестирования НПФ необходимо производить анализ в совокупности по следующим показателям: коэффициенту Шарпа, коэффициенту Трейнора, коэффициенту Альфа Дженсена, коэффициенту Модильяни, модифицированному коэффициенту Шарпа.

Информационная база, используемая для расчетов – статистические данные за период 2016–2020 гг., размещенные на сайте Банка России. При осуществлении расчетов использованы данные по 31 НПФ, осуществляющему на конец 2020 г. деятельность по негосударственному пенсионному обеспечению. Доля пенсионных резервов анализируемых НПФ в общей сумме пенсионных резервов составила на конец 2020 г. 91,5%. Отсутствие рыночных котировок, на основе которых можно было рассчитывать ежедневную доходность НПФ и возможность использования только ежеквартальной статистики, размещаемой на сайте Банком России о деятельности НПФ, приводят к тому, что количество наблюдений значительно сокращается. Это приводит к невозможности использования расчета показателей: коэффициентом Сортино, Омеги, ограничивает возможности использования модифицированного коэффициента Шарпа.

Используемые значения показателей безрисковой доходности и доходности рынка пенсионных резервов приведены в таблице 1. В качестве безрисковой доходности (Rf) использовалась ставка привлечения средств в депозиты ЦБ РФ сроком на один день, которая рассчитывалась на основе данных Банка России. Накопленная безрисковая доходность за период 2016–2020 гг. составила 39,38 %. В качестве доходности рынка пенсионных резервов (Rm) использовалась средневзвешенная по объему пенсионных резервов доходность пенсионных резервов НПФ, осуществляющих негосударственное пенсионное обеспечение. Накопленная доходность рынка пенсионных резервов за 2016–2020 гг., рассчитанная на основе данных сайта Банка России, составила – 39,80%. В методике, используемой агентством АКРА [14] в качестве доходности рынка пенсионных накоплений/резервов используется показатель доходности рынка пенсионных накоплений/резервов, рассчитываемый по 20 крупнейшим НПФ. Однако, исходя из данных таблицы 1, объем выборки в данном случает существенного значения не имеет.

На рисунке 1 представлен разброс соотношений показателей накопленной доходности за 5 лет и коэффициента Шарпа, рассчитанного за этот же период для 31 НПФ, осуществляющих негосударственное пенсионное обеспечение.

На рисунке 1 четко видны 3 группы НПФ. Первая группа – с отрицательным коэффициентом Шарпа – этой группе соответствуют фонды с накопленной доходностью ниже среднерыночной. Вторая – с коэффициентом Шарпа в диапазоне от 0 до 5, третья – выше 5. Рисунок 2 демонстрирует, что анализа эффективности управления портфелями на основе только показателя накопленной доходности недостаточно. Фонды имеющие примерно одинаковые показатели накопленной доходности могут значительно различаться по значению коэффициента Шарпа.

Таблица 1

Расчет накопленной безрисковой доходности и накопленной доходности рынка пенсионных резервов

Источник: составлено авторами на основе [11].

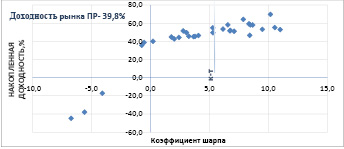
Рис 1. Соотношение показателей накопленной доходности за 5 лет и коэффициента Шарпа по 31 НПФ Источник: составлено авторами на основе [11]

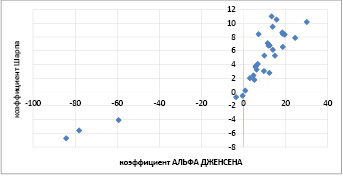
Рис 2. Соотношение показателей коэффициента Шарпа и коэффициента Альфа Дженсена по 31 НПФ Источник: составлено авторами на основе [11]

Таблица 2

Показатели эффективности управления пенсионными резервами НПФ с коэффициентом Шарпа меньше 0

Далее анализ показателей эффективности инвестирования в НПФ будет осуществляться исходя из разделения фондов на данные 3 группы.

В таблицах 2–4 приведены расчеты показателей накопленной доходности и коэффициентов (Кf) Шарпа, Трейнора, Модильяни, Альфы Дженсена, модифицированного коэффициента Шарпа период расчетов – 2016–2020 г. В таблицах 2–4 все анализируемые НПФ проранжированы по степени увеличения коэффициента Шарпа и разбиты, соответственно, разбиты на 3 группы.

1 группа – см. табл. 2 – пять НПФ, с отрицательным коэффициентом Шарпа – от -6,72 до -0,53; с отрицательными значениями коэффициента Альфа Дженсена. Накопленная доходность минимальна по отношению к прочим группам составила от -44,83% до 38,78% соответственно, что значительно ниже среднерыночных показателей. Можно сделать вывод, что инвестиционная стратегия в данных НПФ была разработана неудачно, их деятельность была неэффективной. Самая небольшая по объему пенсионных резервов группа НПФ: доля пенсионных резервов данной группы в их общем объеме на конец 2020 г. составила 5,8%. В данной группе НПФ наблюдается четкая прямая зависимость между основными показателями эффективности управления портфелями пенсионных резервов – рост коэффициента Шарпа приводит к росту накопленной доходности и коэффициента Альфа Дженсена.

Таблица 3

Показатели эффективности управления пенсионными резервами НПФ с положительным коэффициентом Шарпа меньше 5

2 группа – см. табл. 3 – десять НПФ с коэффициентом Шарпа от 0,22 до 4,08. Положительное значение коэффициента Шарпа говорит о том, что данные фонды обогнали среднерыночную доходность, хотя и не показали исключительных результатов. И действительно, накопленная доходность колеблется от 40,06% до 51,54%, что несколько выше среднерыночной, Данные показатели говорят об успешной, хотя может быть консервативной, инвестиционной стратегии. Коэффициент Альфа Дженсена положительный и имеет значительный разброс от 0,90 до 12.37. Рост этого показателя говорит о степени эффективности реализации инвестиционной стратегии НПФ. Наибольшее значение этого показателя за анализируемый период у АО «НПФ «Гефест» – 12,37. Самая набольшая по объему пенсионных резервов группа НПФ: доля пенсионных резервов данной группы фондов в их общем объеме на конец 2020 г. составила 65,2%. В эту группу входят крупнейшие НПФ, такие как АО «НПФ ГАЗФОНД» и АО «НПФ «Благосостояние» и другие.

3 группа – см. табл.3 – наибольшая группа по количеству НПФ (16 фондов). Однако доля данных фондов в совокупном объеме пенсионных резервов составляет только 20,1%. Данные фондов показали наилучшие показатели, характеризующие эффективную инвестиционную стратегию. Накопленная доходность колеблется в районе от 49,56 % до 69,75%, что значительно превышает среднерыночную доходность., т.е. инвестиционная стратегия НПФ, входящих в данную групп была успешной. Коэффициент Шарпа колеблется от 5,29 до 11,01. Альфа положительна и варьируется от 7,17 до 30,08, т.е. НПФ смогли успешно реализовать разработанную инвестиционную стратегию.

Для осуществления сравнения эффективности фондов внутри группы можно использовать коэффициенты Трейнора и Модильяни.

Покажем это на примере сравнения двух фондов из 2 группы с примерно равными уровнями накопленной доходности НПФ «Первый промышленный альянс» и НПФ «Атомгарант».

Таблица 4

Показатели эффективности управления пенсионными резервами НПФ с положительным коэффициентом Шарпа больше 5

Уровень накопленной доходности за 5 лет немного выше 45,63% в НПФ «Первый промышленный альянс» по сравнению с 45,47% в НПФ «Атомгарант». Однако коэффициент Шарпа и коэффициент Модильяни во втором НПФ выше – 3,78 и 46,95 по сравнению с НПФ «Первый промышленный альянс» (3,26 и 45,91 соответственно). При этом деятельность управляющих эффективней в первом НПФ, о чем говорит более высокое значения коэффициента Альфа Дженсена. Отрицательная бета со значением стремящемся к нулю привела к получению отрицательного результата при расчете коэффициента Трейнора. Использование данного коэффициентов при бете, стремящейся к нулю нецелесообразно. И если не принимать во внимание другие показатели, то при выборе НПФ при прочих равных условиях АО НПФ «Атомгарант» для инвестора будет предпочтительней.

При равных уровнях накопленной доходности можно осуществлять и межгрупповые сравнения. Пример ОАО «Межрегиональный НПФ «АКВИЛОН» (уровень накопленной за 5 лет доходности 49,62%) и АО НПФ «Альянс» (49,56%). Первый входит во вторую группу, второй – в третью группу. Коэффициент Шарпа, Альфа Дженсена, коэффициент Модильяни и коэффициент Трейнора во втором НПФ значительно выше. При этом Альфа Дженсена практически равна – 9,69 и 9,89. При выборе НПФ при прочих равных условиях и АО НПФ «Альянс» для инвестора также будет предпочтительней.

Другой пример межгруппового сравнения фондов с примерно одинаковой накопленной доходностью – АО «НПФ «Гефест» (накопленная доходность за 5 лет 51,54%, вторая группа НПФ) и АО Межрегиональный НПФ «БОЛЬШОЙ» (накопленная доходность – 51,11%, третья группа НПФ). При примерно одинаковой накопленной доходности коэффициенты Шарпа (2,78 и 7,11), Модильяни (44,96 и 53,62) и Трейнора (-23,48 и 20,88) выше у второго фонда. Исключение составляет показатель Альфа Дженсена, который незначительно выше у АО «НПФ «Гефест».

При анализе эффективности управления портфелями не может быть использован в качестве критерия только один коэффициент Шарпа. Это подтверждается следующим примером. При анализе фондов с примерно одинаковыми коэффициентами Шарпа АО «НПФ «Ростех» (8,42) и АО «НПФ «Корабел» (8,47) показатели накопленной доходности, Альфы Дженсена, коэффициенты Модильяни и Трейнора значительно выше в НПФ «Корабел» (58,21, 18,59, 56,37 и 31.35 и 46,70, 7,17, 56,25 и 17,91 соответственно).

Заключение

Как видно из проведённого анализа, одного показателя накопленной доходности или одного коэффициента Шарпа недостаточно для оценки эффективности управления портфелем пенсионных резервов/накоплений НПФ. Необходимо в обязательном порядке включения в методики оценки эффективности управления портфелями расчет коэффициента Шарпа и коэффициента Альфа Дженсена. Для осуществления дополнительного анализа, осуществления внутригрупповых и межгрупповых сравнений, формирования дополнительных критериев при формировании ренкингов НПФ и их управляющих компаний могут быть использованы коэффициенты Модильяни и коэффициент Трейнора. Коэффициент Трейнора может быть использован для анализа, только при значении коэффициента бета более 0,1, иначе будет искажать оценку рыночного риска. Оптимальный период расчета – 5 лет. Расчет коэффициентов на больший временной промежуток нецелесообразен. Желательно использовать квартальные оценки доходности. Использование модифицированного коэффициента Шарпа не целесообразно, из-за малого количества наблюдений он будет искажаться.

Описанными выше коэффициентами могут быть дополнены методики оценки надежности НПФ и УК НПФ, осуществляемые как регулятором, так и рейтинговыми агентствами.

Библиографическая ссылка