Введение
Поле экономических отношений находится в постоянном развитии, появляются новые формы кооперации, способы организации экономических пространств, возникают новые модели создания добавочной стоимости. Отчасти, именно этот процесс определяет неустойчивость экономических терминов в тех случаях, кода таковая имеет место быть, что в свою очередь стимулирует развитие и совершенствование теории экономических систем. С учетом имеющегося положительного мирового опыта реализации кластерных концепций достаточно важным является вопрос понимания генезиса и современных изменений кластерных систем. Одновременно с развитием теории кластерных структур происходит ее конвергенция с методологическими аппаратами других наук. В данной работе предлагается рассмотреть подходы к использованию элементов теории графов для построения моделей экономических систем, в частности для выявления кластеров.
В Англии середины девятнадцатого века происходит экономический подъем, на долю страны приходится около половины объема мирового промышленного производства. На смену мануфактурному типу производства приходит фабричный, а ручной труд заменяется машинным. По этой причине происходит быстрое увеличение количества производственных предприятий и приток населения в города. Все это обуславливает возникновение новых форм организации кооперационных связей между экономическими агентами, образование новых типов экономических систем. В 1890 году представителем неоклассической школы экономики А. Маршаллом сформулированы положения относительно новых принципов географического экономического районирования. В работе [1] Маршаллом было введено понятие, характеризующее концентрацию производственных мощностей в рамках единой географической территории, такое замкнутое образование определялось им как промышленный район. Так или иначе, в ситуации сегодняшнего дня, генезис предметной области, связанной с вопросами промышленных агломераций, основывается на работах А. Маршалла, а современные теории включают в себя три базовых фактора повышения производительности труда – единый рынок квалифицированной рабочей силы, локальную торговлю между фирмами и территориальное разделение труда. В работах М. Вебера [2] организация промышленного производства представлена с точки зрения эффективности построения горизонтальной партнерской сети, выявлены экономические, исторические, культурные факторы возникновения экономических агломераций. Однако, на сегодняшний день понятие экономических кластеров тесно связано с именем М. Портера. Портером предложена модель повышения эффективности национальной экономики по средствам управления изменениями цепочек создания добавленной стоимости предприятий. По Портеру существует три уровня конкуренции – конкуренция между предприятиями, на уровне отраслей и между странами. Конкурентоспособность как предприятия, так и страны определяется при этом следующими условиями – параметрами спроса, параметрами факторов, стратегиями фирм и их структурой, родственными и поддерживающими отраслями. Четыре этих параметра образуют ромб Портера, устойчивость и гибкость которого может быть достигнута по средствам реализации кооперационных отношений между фирмами по кластерному типу. Такой тип позволяет максимизировать интенсивность инновационных процессов, увеличить количество вновь создаваемых компаний, горизонтальных связей и их гибкость, повысить конкурентоспособность предприятий и национальной экономики в целом. В течении исторического процесса происходит развитие экономики, а, следовательно, и увеличение сложности организации экономических систем.
Цель исследования. Представляется интересным выявить новые подходы к рассмотрению кластерных систем, новые инструменты анализа их функционирования, в том числе выявления кластерных систем. В данной работе предлагается рассмотреть особенности современных экономических кластеров и с учетом этих особенностей рассмотреть возможные варианты выявления кластеров. Предлагается рассмотреть экономические системы, в том числе кластерные, как социальные графы, содержащую в себе информацию об агентах и отношениях между ними. В частности, это позволит рассмотреть подходы к выявлению экономических кластеров с помощью алгоритмов теории графов.
Материал и методы исследования
На сегодняшний день существует большое количество подходов к определению понятия экономический кластер и выявлению кластерных структур. Портер определяет кластер как «сконцентрированные по географическому признаку группы взаимосвязанных компаний, специализированных поставщиков, фирм в соответствующих отраслях, а также связанных с их деятельностью организаций (университетов, агентств по стандартизации, торговых объединений и пр.) в определенных областях, конкурирующих, но вместе с тем и ведущих совместную работу» [4]. В этой работе со ссылками на исследования Т. Андерссона [6], Г. Бекаттини [7] приведен анализ классификаций и определений кластерных структур. В целом, исследователи приходят к выделению двух аспектов понимания кластерной системы. Первый из них – это классический, Портеровский, в рамках которого экономическая система детерминируется как кластер, если ей присущи такие свойства как: 1) географическая концентрация агентов, свобода участников и интегрированность в единую цепочку создания добавленной стоимости. Второй аспект понимания кластерной системы связан с изменениями, происходящими в мировой экономике сопряженными с переходом к постиндустриальному типу взаимодействия экономических агентов. Как об этом сказано в работе [8] кластер в данном понимании не рассматривается как структурное образование, состояние определенных взаимоотношений участников выступают сутью кластера. В работе [9] подчеркивается, что базовым предметом экономических отношений агентов – участников кластера становятся знания. Одним из кластерных признаков становиться степень интенсивности обмена информацией между агентами. Здесь, традиционное понимание географической близости расширяется за счет следующего набора, задающего степень плотности взаимодействия: когнитивная близость, организационная близость, социальная близость, институциональная и технологическая близость [10]. Практики понимания кластерных систем именно в контексте экономики знаний стали сегодня широко распространены для европейских и американских экономистов [11,12]. Именно такие подходы к детерминации экономического кластера определили способы выявления кластерных структур. В частности, существует подход, основанный на расчете индекса П. Кругмана [13], который дает оценку концентрации промышленности в регионе. Данная модель сопрягается с традиционным пониманием кластерных систем и основывается на выявлении доли рабочих мест, занятых в соответствующем секторе промышленности. Модель изначально была разработана как метод выявления агломераций в условиях монополистической конкуренции и экономии от масштаба. Распространенным способом оценки степени экономической активности служит метод Лоранца [14] разработанный для расчета показателя неравенства доходов населения. Данная модель может быть применена для выявления подсистем экономических агентов и их распределение по степени экономической активности [15]. Индекс Эллисон-Глэйсер имеет широкое распространение для оценки степени концентрации экономической активности на территории. Данный коэффициент так же основан на значениях общего количества рабочих мест на территории и рабочих мест, занятых в отрасли. Вообще, стоит отметить, что все приведенные выше методики выявления экономических кластеров имеют допущения свойственные моделям традиционного понимания кластерных систем:
1) Географическая концентрация экономических агентов. На основе предлагаемых известными методиками выявления экономических кластеров определяется степень концентрации агентов на территории, их близость и интенсивность взаимодействия.
2) Предполагается, что участники экономического кластера принадлежат к одной отрасли. Это достаточно очевидный факт, однако при определении количества участников кластера и его величины вообще могут быть упущены из анализа часть агентов, осуществляющих вспомогательные или непрофильные функции в рамках кластера.
3) Зачастую модели выявления кластерных систем основываются на предположении о том, что предметом хозяйственных отношений между участниками кластера являются материальные активы.
Таким образом, большинство существующих моделей выявления экономических кластеров и агломераций в целом адекватны для традиционного понимания кластерной системы. Одновременно с тем, может быть упущены из вида свойственные для современного типа экономики отношения между агентами основанные на перераспределение информации.
Результаты исследования и их обсуждение
В условиях современной цифровизации любая система, в том числе кластерная может быть описана как набор информации о ее элементах и отношений между ними. [16,17]. Поэтому экономическая система, а в частности кластерная система могут быть рассмотрены как модальность, состоящая из множества агентов (производственных и услуговых организаций, финансовых и научных институтов) и определенном на нем множестве отношений между ними. Такая модель может быть представлена как граф с направленными ребрами. Данный подход к моделированию экономической системы позволяет воспользоваться обширным методологическим аппаратом, разработанным в рамках теории социальных графов [18,19]. Социальный граф представляет из себя не четко заданный математический конструкт, а скорее объект, обладающий набором характеристик [20]:
- Большая компонента связности – практически от любого агента можно через ребра связности попасть к другому агенту, агенты в данной модели представляют из себя вершины графа.
- В среднем, для графа экономической системы, в особенности кластера, среднее количество переходов, которые необходимо совершить между вершинами не велико. Это же утверждение справедливо для социального графа.
- В социальном графе с большой долей вероятности, если первая вершина соединена со второй, а вторая с третьей, то первая вершина так же будет соединена с третьей. Для случая экономической системы это говорит о высокой плотности кооперационных связей и наличии сообществ внутри системы.
- Структура, основанная на сообществах. Эта особенность социального графа на ряду с выше перечисленными позволяет предложить метод выявления экономических агломераций и кластеров.
Мы можем сделать предположение о том, что экономические системы представимы в виде графа, где агенты являются вершинами графа, а связи между ними направленными ребрами. Причем, кластерные структуры являются сообществами внутри такого рода социальных графов. Тогда представляется возможным использование алгоритма выявления сообществ внутри социальных графов. Одним из распространенных подходов [21] к выявлению и оценки степени разбиения графа на сообщества является метод основанный на расчете модулярности Ньюмана-Гирвана [22]. В рамках данной методики предполагаются следующие допущения:
- существуют подгруппы экономической системы, плотность взаимодействия участников которых выше, чем средняя в системе и выше
- плотность взаимодействия между участниками подгрупп выше, чем если бы кооперационные связи между участниками всей системы были распределены случайным образом.
В основе метода лежит понятие модулярности, величины, рассчитываемой как доля ребер, которые попадают в заданную подгруппу за вычетом доли ребер, в случае, если бы связи были распределены случайным образом. Данная величина для случая экономических систем характеризует на сколько плотность отношений в подгруппе образованной участниками кластера выше случайного базового значения.
Значение модулярности определяется следующим образом:
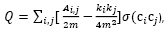
где m –количество кооперационных связей внутри экономической системы, A – матрица смежности графа экономической системы, Ai,j – наличие связей между участниками i и j, ki – степень вершины i, другими словами, количество экономических связей, которое имеет участник i, ci – номер класса (подгруппы), к которому принадлежит вершина i. Данный метод достаточно хорошо разработан в теории графов [17] и представляет из себя итерационный алгоритм, состоящий их двух фаз. На первой фазе каждому участнику экономической системы ставится в соответствие вершина графа, а каждая вершина в свою очередь считается отдельным сообществом. Затем, рассматривается каждая вершина и рассчитывается прирост модулярности при удалении вершины и добавлении ее в каждое сообщество из окружающих ее вершин. Вершина перемещается в то сообщество, для которого прирост составил максимальное значение, если такого не произошло, то вершина остается на своем месте. На второй фазе строится новый граф уже с измененным положением вершин, и процедура повторяется снова. В качестве апробации подхода рассмотрим экономическую систему из предприятий, локализованных в Ульяновске и расположенных на территории промышленной зоны. Для простоты не будем учитывать объем хозяйственных операций, осуществляющихся между ними, а только сам факт наличия экономической связи. Рассмотрим выборку из 22 компаний и для каждой из них рассчитаем коэффициент модулярности. Названия компаний из соображений коммерческой тайны не указываются. В таблице ниже представлена матрица смежности для данной экономической системы.
По средствам программы Gephi был построен граф данной модели и рассчитаны значения модулярности для каждого из участников. Цветом выделены узлы графа – участники экономической системы, плотность кооперации которых выше в сравнении с другими участниками системы. Мера модулярности для данной системы составляет 0,438. Данный подход только иллюстрирует принцип работы алгоритма определения подграфов для случая выявления кластеров в экономических системах. Однако, понятно, что представление экономической системы, в частности кластера в виде графа позволяют выявить статистику и особенности структуры кооперационных отношений – выявить подгруппы, кластеры, плотность кооперационных отношений.
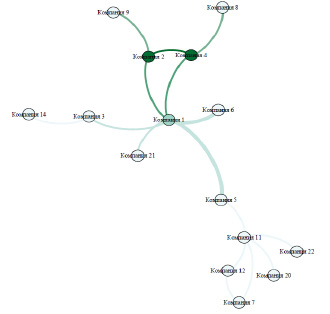
Рис. 1. Граф экономической системы
Таблица 1
Матрица смежности компания – участников экономической систем
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
11 |
12 |
14 |
20 |
22 |
|
|
1 |
1 |
1 |
1 |
|||||||||||
|
2 |
1 |
1 |
1 |
|||||||||||
|
3 |
1 |
1 |
||||||||||||
|
4 |
1 |
1 |
1 |
|||||||||||
|
5 |
||||||||||||||
|
6 |
1 |
|||||||||||||
|
7 |
1 |
1 |
||||||||||||
|
8 |
1 |
|||||||||||||
|
9 |
1 |
|||||||||||||
|
10 |
||||||||||||||
|
11 |
1 |
1 |
1 |
1 |
1 |
|||||||||
|
12 |
1 |
1 |
||||||||||||
|
13 |
||||||||||||||
|
14 |
1 |
|||||||||||||
|
15 |
||||||||||||||
|
16 |
||||||||||||||
|
17 |
||||||||||||||
|
18 |
||||||||||||||
|
19 |
||||||||||||||
|
20 |
1 |
|||||||||||||
|
21 |
1 |
|||||||||||||
|
22 |
1 |
Выводы или заключение
Понятие экономический кластер с течением времени усложняется и начинает включать в себя все большее количество смысловых уровней. Изначально понятие кластер выходит из теории промышленных районов и экономических агломераций и тесно с ними связано, Портером предлагается новый подход к определению кластера, как саморазвивающейся экономической системы, участники которой взаимодействуя по кластерному типу между собой, со внешними агентами под воздействием экстерналий увеличивают свою конкурентоспособность и системы в целом. На сегодняшний день информация становится одним из основных факторов производства. Кроме того, бизнес процессы активно оцифровываются, в результате чего хозяйственная деятельность экономических субъектов и их систем может быть представлена как набор динамических матриц. Таким образом, экономическая система может быть рассмотрена как граф, вершины которого представляют собой экономических агентов, а ребра характеризуют кооперационные связи между ними. В работе предложена модель выявления кластерных структур в экономических системах, основанная на алгоритме поиска подгрупп в социальных графах. В дальнейшим представляется интересным рассмотреть работу метода выявления для более сложных систем с учетом весов узлов графа – размеров компании и интенсивности хозяйственной деятельности.
Библиографическая ссылка
Синицын А.О., Цыганцов А.В. ВЫЯВЛЕНИЕ ЭКОНОМИЧЕСКИХ КЛАСТЕРОВ КАК ПОДГРУПП ЭКОНОМИЧЕСКИХ СИСТЕМ // Вестник Алтайской академии экономики и права. 2018. № 8. С. 220-225;URL: https://vaael.ru/ru/article/view?id=224 (дата обращения: 02.03.2026).

