Разработан универсальный алгоритм численной оценки качества объекта на основе данных экспертов. На практике этот алгоритм можно использовать для оценки качества любого предмета, процесса, явления, где оценка качества затруднена без привлечения мнений экспертов. Структура исследуемой системы представляется в виде графа, где в качестве узлов приняты основные составляющие этой системы. Качество каждой подсистемы характеризуется множеством параметров. Значения этих параметров оцениваются экспертами и сводятся в одну таблицу. На основе данных этой таблицы строятся диаграммы качества подсистем, а также вычисляется интегральный показатель качества как среднее геометрическое. По этим же правилам вычисляется значение показателя качества всей системы в целом. Расчеты по оценке качества объекта полностью формализованы, что в результате позволяет эти расчеты автоматизировать, т.е. разработать соответствующие алгоритмы и программное обеспечение. Создан виртуальный центр (сайт), на базе которого проходят экспертизу на оценку качества on-line учебные курсы еще до начала их эксплуатации. Опыт показывает, что такой подход позволяет сформировать эффективную реально - виртуальную образовательную среду вуза для подготовки студентов по любым направлениям подготовки, а также включить систему контроля качества в единую систему «Электронный Вуз».
Введение
С организацией (самоорганизацией) реально-виртуальной образовательной среды и как следствие с появлением on-line курсов изменились роли всех участников образовательного процесса. При этом педагог превратился в руководителя, студент в самостоятельного обучающегося, а компьютер в инструмент коммуникации, обеспечивающий «искусственный интеллект», вычислительную работу, интерактивность и мониторинг за процессом подготовки студента.
В то же время, потребность в эффективной подготовке в быстром темпе в технологичном «мире», с использованием вычислительной техники в новой реально-виртуальной среде, породило множество специфичных педагогических проблем. На практике стало очевидно, что эти проблемы можно разрешить только в интеграции педагогических, психологических и инженерных методов. В результате сформировалась новая методология с названием дидактическая инженерия [1-4], нацеленная на эффективную организацию деятельности всех участников образовательного процесса в реально-виртуальной среде.
Следует отметить, что все проблемы в предложенной классификации Г. Саймоном, подразделяются на три класса:
1) хорошо структурированные или количественно сформулированные проблемы, в которых существенные зависимости выяснены настолько хорошо, что они могут быть выражены в числах или символах, получающих, в конце концов, численные оценки;
2) неструктуризованные или качественно выраженные проблемы, содержащие лишь описание важнейших ресурсов, признаков и характеристик, количественные зависимости между которыми совершенно неизвестны;
3) слабоструктуризованные или смешанные проблемы, которые содержат как качественные, так и количественные элементы, причем качественные, малоизвестные и неопределенные стороны проблем имеют тенденцию доминировать.
Для решения неструктурированных проблем куда и относятся многие педагогические, используются методы экспертных оценок, когда математическая формализация проблемы затруднена в силу их новизны и сложности, либо требуют больших затрат и средств.
Общим подходом для всех методов экспертных оценок является обращение к опыту экспертов, на основе которых зарождаются в определенной степени формализованные методы и алгоритмы, позволяющие автоматизировать процесс принятие решений с использованием вычислительной техники.
В работе рассматривается случай, когда учебный курс представляет собой сложную замкнутую информационную систему, нацеленную и предназначенную для освоения какой-то компетенции. При этом очевидно, что разные курсы в зависимости от их качества организации, содержания, формы, сложности обладают разным обучающим потенциалом (в смысле возможностями) для освоения требуемой компетенции. В этой ситуации актуализируется необходимость разрешения следующей проблемы.
Цель исследования. Требуется до начала эксплуатации рассматриваемого экземпляра on-line курса оценить его обучающий потенциал, т.е. его качество с точки зрения достижения цели (освоение компетенций) через обучение.
Материал и методы исследования
Обучающий потенциал on-line курса, как любой сложной системы, зависит от потенциала его подсистем. В свою очередь, потенциал любой подсистемы зависит от множества скрытых (латентных) и расчетных (метрических) показателей этих подсистем.
Очевидно, что на практике, оценить значение скрытых показателей может только эксперт, например, такие показатели как валидность и релевантность вопросов теста. Что касается расчетных показателей, то их значением метрик, также можно оценить, исходя из данных трудозатрат экспертов, например, сложность теста можно оценить по продолжительности ответов на них эксперта, продолжительность процесса тестирования для студента можно вычислить, исходя из значения показателя сложности теста [5] и т.д.
Модель on-line курса. В общем случае, структурная модель on-line курса может быть представлена в виде сетевого графа (рис.1).
Согласно рис. 1, в УОК выделены четыре взаимосвязанных подсистемы: ТМ, ПМ, ДМ, ИК.
При вычислении значения показателя качества УОК, с учетом качества всех его подсистем, изначально используется принцип равных влияний, т.е. качество каждой подсистемы равным образом влияет на образование качества УОК в целом. На концептуальном уровне эту зависимость показателя качества УОК от показателей качества ее компонент ТМ, ПМ, ДМ и ИК можно записать как функциональную зависимость, т.е.
УОК = F(ТМ, ПМ, ДМ, ИК).
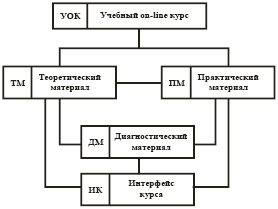
Рис. 1. Структурная модель УОК
В модели также вводятся нормировочные ограничения: значения показателей качества УОК ТМ, ПМ, ДМ, ИК, изменяются почти от 0 до 1, т.е. в интервале за исключением нуля (0, 1). Таким образом, у идеального экземпляра УОК, т.е. у курса наивысшего качества будут все значения показателей равными 1 или имеют 100% значение показателя качества. Формально, в наших условиях и обозначениях, можно записать так
УОК = 1 = F(1, 1, 1, 1).
Аналогично, любые значения показателей качества подсистем: ТМ, ПМ, ДМ, ИК могут быть детализованы на следующем иерархическом уровне со своими показательными параметрами, т.е. t(*), n(*), g(*), u(*). Сами подсистемы (аналогично системе) могут быть представлены так
ТМ = F1(t(1), …, t(*), …, t(k1))
ПМ = F2(n(1), …, n(*), …, n(k2))
ДМ = F3(g(1), …, g(*), …, g(k3))
ИК = F4(u(1), …, u(*), …, u(k4)),
где компоненты t(*), n(*), g(*), u(*) подчиняются ограничению (0, 1).
Следует отметить, что эту декомпозицию метрических оценок качества подсистем можно продолжить до практически необходимого уровня детализации. При этом, на любом иерархическом уровне организации оценки качества, значения показателей этого качества изменяются в пределах (0, 1].
Среднее геометрическое как метрика показателя качества УОК. Всем принятым в модели ограничениям удовлетворяет функция «среднее геометрическое», т.е. функция вида
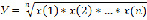
при ограничениях 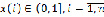 .
.
Конкретно рассмотрим только двухуровневую модель для оценки качества УОК. В наших обозначениях эта модель выглядит так:
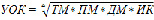
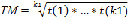
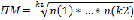
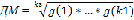
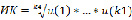 ,
,
где k1, k2, k3, k4 – количество характеризующих параметров у подсистем.
Таким образом, оценка качества любого объекта сводится к задаче вычисления среднего геометрического всех узлов сети (рис. 1) с соблюдением иерархии уровней организации.
На практике возникает резонный вопрос: почему надо использовать функцию «среднее геометрическое», а не, например, среднее арифметическое для оценки качества объекта. Приведем пример: допустим качество какой – то системы СИ зависит от ее составляющих С и И. При этом известно, что качество С = 0,9, а качество И = 0,1. По принятому правилу расчета качество СИ (по среднему геометрическому) равно 0,3, а по среднему арифметическому 0,5. Таким образом, среднее геометрическое «умеет» ловить системы с низким качеством одного из составляющих компонент и отражать ее на оценке качества всей системы. Это делает систему оценки более валидной и надежной [1] в функциональной среде систем.
Пример оценки качества УОК. Для того, чтобы оценить качество УОК в целом, необходимо оценить качество его компонент: ТМ – теоретического материала, ПМ – практического материала, ДМ – дидактического материала, ИК – интерфейса курса.
Особо подчеркнем, что, качество всех компонент УОК оценивается по одному и тому же рекурсивному алгоритму, поэтому вполне достаточно подробно привести расчет значения показателя качества одной из подсистем, например, ДМ, а качество других компонент УОК, т.е. ТМ, ПМ, ИК будет оцениваться аналогично.
Согласно разработанной модели качество ДМ будет оценено по формуле
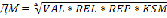 .
.
В этой формуле приняты обозначения: VAL – валидность (адекватность и пригодность) комплекса вопросов, предложенных студенту в тесте; REL – релевантность вопросов теста, т.е. спрашивается ли в них то, что изложено в рамках курса; REP – репрезентативность вопросов теста, т.е. равным ли образом представлены вопросы в тесте из всех разделов курса; KSM – качество полноты и целостности комплекса вопросов, т.е.представлены ли в тесте одинаковое количество вопросов на знание «фактов» и на знание «связей» в изучаемой предметной области. На практике, оценку качества теста по критериям VAL, REL, REP, KSM могут оценить эксперты в процессе исследования предложенного экземпляра УОК.
Алгоритм оценки качества ДМ. Допустим, качество ДМ как подсистемы УОК, оценивают шесть экспертов независимо друг от друга. Результаты представлены на рис. 2.
|
Эксперты Критерии |
1 |
2 |
3 |
4 |
5 |
6 |
Среднее значение |
|
VAL |
0,9 |
0,8 |
0,6 |
0,9 |
0,7 |
0,9 |
0,8 |
|
REL |
0,8 |
0,7 |
0,8 |
0,7 |
0,7 |
1 |
0,783 |
|
REP |
0,8 |
0,7 |
0,7 |
0,8 |
0,8 |
1 |
0,8 |
|
KSM |
0,7 |
0,8 |
0,7 |
0,6 |
0,7 |
1 |
0,75 |
Рис. 2. Данные экспертных оценок качества теста учебного курса
По данным (рис. 2) в единичном круге построена диаграмма Кивиата для демонстрации качества дидактического материала по разным критериям (рис. 3).
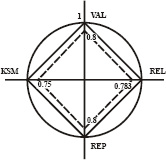
Рис. 3. Диаграмма Кивиата
для визуализации состояния качества дидактического материала учебного курса
Согласно модели, интегральную оценку качества ДМ можно вычислить как среднее геометрическое, т.е.
ДМ = F3(VAL, REL, PER, KSM) ;
ДМ = 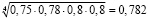 .
.
Таким образом, качество ДМ в рассматриваемом курсе 78% из 100% возможных. В принятой вузовской шкале, качество ДМ оценивается как «отличное». Следует отметить, что результаты работы экспертной группы, полученные в ходе анкетирования должны пройти обязательную проверку на согласованность. Если мнения экспертов окажутся несогласованными, т.е. мнения существенно отличаются друг от друга внутри группы, то результаты признаются непригодными для вынесения обоснованного решения, например, купить или не покупать этот экземпляр УОК. При этом сама экспертиза считается с сомнительными результатами.
В этом случае, для лица принимающего решения (ЛПР), возможно два варианта действия:
1. Пригласить новую команду экспертов, так как может быть квалификация экспертов «старой команды» сильно отличается и поэтому у них разные критерии оценки качества.
2. В рамках «старой команды» использовать метод Дельфи (авторы этого метода О. Холмер, Т. Гордон, США). Как известно этот метод позволяет получить согласованные значения оценок в процессе анонимного обмена мнениями между участниками группы экспертов и на базе этих мнений принять решения в зависимости от ситуации:
2.1. Если ДМ, т.е. дидактический материал, создан вами, то учитывая мнения экспертов можно изменить содержание и переформатировать этот материал.
2.2. Отказаться в целом от приобретения этого экземпляра УОК в виду сомнительного качества ДМ.
Формализованным общепринятым методом проверки согласованности мнений экспертов является метод, основанный на вычислении коэффициента множественной ранговой корреляции Кендалла – Смита, так называемого коэффициента конкордации с проверкой его статической значимости.
Для проведения процедуры проверки согласованности мнений экспертов, представленные ими данные, ранжируются по следующим правилам: самой высокой оценки присваивается ранг 1, следующей – 2 и т.д. Одинаковым оценкам присваиваются одинаковые ранги, равные среднему арифметическому их порядковых номеров. Такие ранги называются связанными. Сводные таблицы ранжирования представлены на рис. 4.
Для вычисления коэффициента конкордации K (Кендалла-Смита) воспользуемся известным соотношением
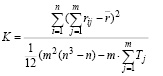
где rij- ранг i – ого показателя у j-ого эксперта:
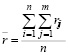
где n – число оцениваемых показателей; m – число экспертов в составе группы.
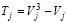
где Vj – количество одинаковых связанных рангов, выставленных j-ым экспертом.
Используя расчетные соотношения, получим
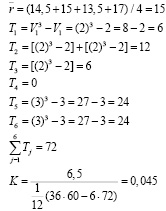
Визуальная оценка значения коэффициента К позволяет предположить, что мнения экспертов не согласованное, т.е. сделать вывод о несогласованности экспертных оценок. Тем не менее, чтобы в этом убедиться, проверим гипотезу согласованности статистики по критерию χ2.
|
Эксперты Критерии |
1 |
2 |
3 |
4 |
5 |
6 |
Σ |
|
VAL |
1 |
1,5 |
4 |
1 |
3 |
4 |
14,5 |
|
REL |
2,5 |
3,5 |
1 |
3 |
3 |
2 |
15 |
|
REP |
2,5 |
3,5 |
2,5 |
2 |
1 |
2 |
13,5 |
|
KSM |
4 |
1,5 |
2,5 |
4 |
3 |
2 |
17 |
Рис. 4. Сводная карта ранговых оценок
Для этого воспользуемся формулой
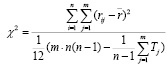 .
.
В рассматриваемом случае
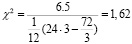 .
.
Сравним эту величину с табличным значением критерия для уровня значимости a= 0,05 степень свободы f = 3;
χ2 (таб)= 7,8 > 1,62. Из этого можно сделать вывод, что мнение экспертов не согласованное, относительно «отличного» качества теста. Разумеется, это снижает надежность оценки теста, т.е. мнение экспертов разошлись, и верить этой оценке сомнительно.
Результаты исследования
и их обсуждение
Оценка качества УОК. Допустим, в рассматриваемом случае ЛПР использовал метод Дельфи (см. пункт 2.1 по тексту) и авторы переделали подсистему ДМ (с точки зрения повышения ее качества), а затем повторно эта подсистема прошли экспертизу с результатами: мнение экспертов согласованное; ДМ = 0,873. Далее, на практике по аналогии с нашими вычислениями, эксперты оценили качество всех компонентов у системы УОК. При этом получили следующие результаты: ТМ = 0,613 (мнение согласованное); ПМ = 0,73 (мнение согласованное); ИК = 0,66 (мнение согласованное).
Для наглядного представления результатов построим диаграмму Кивиата (рис. 5).
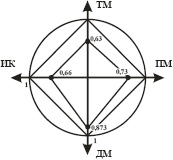
Рис. 5. Диаграмма Кивиата
для визуализации состояния качества УОК
В целом, численное значение показатель качества УОК вычисляется так:
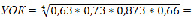
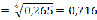 .
.
Полученный результат показывает, что образовательный потенциал учебного on-line курса (УОК), примерно, составляет 72% из возможных 100%.
Очевидно, что при этом значении показателя качества, ЛПР решает: искать лучший вариант УОК или нет.
Заключение
Рассмотренный алгоритм оценки качества (в данном случае образовательный потенциал) объекта УОК является универсальным. На основе данных экспертов его можно использовать во всех областях человеческой деятельности для оценки качества любого объекта, т.е. предмета, процесса, явления.
Библиографическая ссылка
Старыгина С.Д., Нуриев Н.К. АЛГОРИТМ ЧИСЛЕННОЙ ОЦЕНКИ КАЧЕСТВА ON-LINE КУРСА // Вестник Алтайской академии экономики и права. 2018. № 1. С. 55-60;URL: https://vaael.ru/ru/article/view?id=22 (дата обращения: 10.03.2026).

