Введение
Логистика является достаточно молодой наукой, которая имеет глубокие исторические истоки. Считается, что сам термин имеет древнегреческое происхождение и обозначал «счетное искусство». В настоящее время вопросами, связанными с логистическими системами, занимаются многие отечественные и зарубежные ученые. Так, например, в работе [10] В.И. Хабаровым, А.А. Теселкиным, К.П. Косолаповым описано планирование экспериментов для оценки матрицы транспортных корреспонденций; оптимизация логистических процессов в Арктической зоне предложена в монографии наших коллег [6]; Елсуковым П.Ю. и Цветковым В.Я. в [3] предложена аналитическая модель, описывающая жизненный цикл сложной системы с использованием логистического уравнения; Коробовым В.Б., Тутыгиным А.Г., Чижовой Л.А. разработан подход, основанный на последовательном принятии решений, для минимизации ошибки выбора наиболее экономически эффективной и экологически безопасной альтернативы при принятии стратегических решений проектирования транспортной инфраструктуры в Арктике [5, 7]; ими же описаны ограничения на стандартные модели морских логистических операций в Арктике [8].
Основной целью логистики является получение максимальной эффективности при минимальных затратах. Существует множество видов логистики: закупочная, транспортная, распределительная и так далее. В соответствии с этим определяются типы логистических систем, каждая из которых обладает своим жизненным циклом.
Этапы жизненного цикла логистической системы зависят от объемов продажи товаров или объемов оказания услуг, а также от прибыли компании. Обычно жизненный цикл логистической системы описывают S-образной моделью, включающей в себя два эволюционных цикла. Данный вид модели был впервые предложен П.-Ф. Ферхюльстом в конце 19 века, а затем Р.Перлем и Л. Ридом в 20-х годах 20-го века. Первый цикл по данной модели представляет собой зарождение и развитие системы, а также ее зрелость. На этапе создания организации можно выделить такие характеристики управления, как постановка нечётких целей, а также наличие высоких творческих возможностей. Рост системы связан с формализацией правил и высокими обязательствами, которые также свойственны и на этапе зрелости компании. Помимо этого, этап зрелости характеризуется стабильной структурой и особым упором на эффективность. Второй же цикл начинается с момента спада прибыльности компании и заканчивается ликвидацией логистической системы. При этом компания характеризуется высокой текучестью кадров и возрастающими внутренними и внешними конфликтами. Оба этих циклы характеризуются количественными и качественными параметрами системы при неизменных принципах построения логистической системы. Деятельность таких предприятий зависит от множества экономических и естественных факторов. На успешность развития данных организаций влияют климатические условия, инфраструктурное обеспечение, конкуренция и множество других факторов.
Одной из современных концепций формирования логистических организаций является концепция популяционной экологии, принципами которой являются следующие утверждения:
1. В соответствии с направлением и содержанием экономической деятельности можно выделить популяции логистических систем одного типа.
2. Существует предельная величина емкости ниши, то есть сегмента рынка.
3. Логистические организации «рождаются» и «умирают» по законам популяции.
Одним из современных методов исследования популяционных моделей является модель Соле-Манрубиа [1]. Данная модель основана на четкой логике. Однако, следует отметить, что в силу высокой субъективности вопросов, связанных с экономическим состоянием каждой из систем, а также взаимодействия систем между собой, а также ограничений области действий в рамках описанной модели, применение нечетких отношений придаст большую реалистичность, что позволит получить наиболее адекватную модель.
Целью данного исследования является применение модели Соле-Манрубиа к совокупности логистических систем и разработка модификации эволюционной модели для учета стохастического характера формирования вектора состояния системы в каждый момент времени. Для достижения поставленной цели используется теория нечетких множеств. При этом планируется построить имитационную модель жизненного цикла совокупности логистических систем, которая определяет количество продолжающих функционирование компаний, а также количество прекративших свою деятельность организаций в каждую единицу модельного времени.
Материалы и методы решения
Для оценки экономического состояния логистической системы оценивается интегральный показатель логистического менеджмента [2]. Совокупность логистических компании представляет собой социо-экономическую систему для моделирования которой удобнее использовать мультиагентное моделирование, представив компании как набор автономных, неоднородных агентов, обладающих определенной информацией и действующих в условиях неопределенности, расположенных в определенной «среде обитания» [7]. При этом рассматриваются различные параметры, представляющие собой разнородную информацию, полученную от экспертов и представленную в виде логистических переменных, а также различные количественные показатели, определяемые в ходе оперативной деятельности предприятия. Данные показатели являются разнородными не только по формате, но и по времени их получения. Таким образом, для того чтобы обобщить всю эту информацию, и использовать в оценке состояния логистической системы удобнее использовать нечеткие числа с определенными функциями принадлежности.
Говоря о нечетких числах, предполагают работу с нечеткими множествами. Особенности работы с нечеткими характеристиками представлены в работе [11]. Данный термин был определен американским ученым Л.Заде. При этом, понятие классического множества, где однозначно определяется принадлежность элемента множеству, расширяется. Если элемент принадлежит классическому множеству, то функция принадлежности будет принимать значение 1, а если не принадлежит, то 0. В нечетком множестве, значение функции принадлежности принимает более двух значений. Таким образом, указанная функция может заполнять весь отрезок [0,1].
Определение. Нечетким множеством A называют пару (U, μА(и)), где U – универсальное множество, μА(и) – функция, определенная на множестве U и принимающая значения на отрезке [0,1]. Функцию μА(и) называют функцией принадлежности нечеткого множества A [4].
Если универсальное множество, на котором определена функция принадлежности нечеткого множества конечно или счетно, то
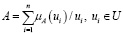
Определение. Нечетким числом X называют нечеткое подмножество А множества действительных чисел R.
Множество R является универсальным множеством, его промежуток [a1,a2] – носителем множества A, на R задана функция принадлежности нечеткого числа μА(х) → [0,1], х ∈ R, принимающая на (a1,a2) положительные значения, а в остальных точках числовой оси равная нулю.
Представим логистические организации как некоторую систему, состоящая из n видов компаний. Экономическое состояние каждой компании представлено нечётким числом xi с функцией принадлежности нечёткого множества A и помеченным индексом 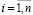 , μА(xi): X → [0,1], где X – универсальное множество. Нечёткое множество А можно определить как «выживаемость» предприятия. Главной характеристикой состояния системы в модели Соле-Манрубиа является n-мерный вектор Ω:
, μА(xi): X → [0,1], где X – универсальное множество. Нечёткое множество А можно определить как «выживаемость» предприятия. Главной характеристикой состояния системы в модели Соле-Манрубиа является n-мерный вектор Ω:
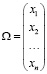
Если xi = 0, то i-я компания прекратила свою деятельность, если xi = 1, то данная компания находится в хорошей ситуации с экономической точки зрения.
Предположим, что в начальный момент времени все рассматриваемые компании находятся в хорошей экономической ситуации, то есть,
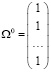
Кооперативные взаимодействия между предприятиями фиксируются матрицей взаимодействия Mk, размерности (n×n), которая в нулевой момент времени совпадает с единичной матрицей. Каждый элемент матрицы mij обозначает влияние организации j на организацию i.
Если mij>0, а mji<0, то i-я компания отрицательно влияет на j-ю компанию.
Если mij>0, mji>0, то оба предприятия сотрудничают.
Если mij<0, mji<0, то оба предприятия конкурируют.
Динамика системы заключается в изменении состояний системы, то есть в определении состояния системы в момент времени (t+1), зная параметры состояния системы в момент времени t. В конце каждого периода k состояние системы фиксируется и обозначается как Ωk. Интерес представляет динамика вектора Ωk, а именно количество ненулевых элементов данного вектора в каждый момент времени. Данное изменение можно представить в следующих шагах:
1. В период времени k матрица Mk получается из Mk-1, путем замены в каждой строке этой матрицы случайно выбранного одного элемента, не лежащего на диагонали, (независимо от его предыдущей величины и знака) на новое случайное значение aij случайной величины, равномерно распределенной в отрезке [-1, 1]. Так, например, для первого периода времени матрица M1 может принять вид:
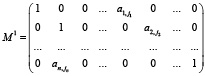
2. Новое состояние каждого вида определяется следующим образом: полученная матрица умножается справа на единичный вектор размерности n в результате чего получается вектор ωk, 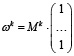 .
.
Для формирования вектора Ωk+1 будем использовать кусочно-линейную функцию принадлежности μА, где
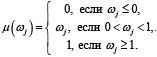
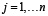
Тогда получаем вектор Ωk+1:
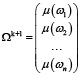
3. Все ниши, оставленные свободными из-за прекращения деятельности какой-либо логистической компании, заполняются копиями одного из случайно выбранных компаний, продолживших свою деятельность. Для этого случайным равновероятным образом выбирается одна из функционирующих компаний j и для всех компаний i, которые в данный период прекратили деятельность, в матрице Mk, осуществляется замена:
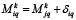
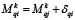
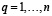
где δiq – случайные равномерно распределенные величины в пределах (-0,01;0,01).
Таким образом, на начальных этапах жизнедеятельности системы, она подвергается эволюции. Матрица взаимодействия всё менее становится похожей на единичную матрицу, а все большей и большей степени отображает реальное взаимодействие между логистическими компаниями в каждый определенный момент времени.
Результаты исследования и их обсуждение
На основе представленного алгоритма были выполнены численные эксперименты с использованием объектно-ориентированного языка Python. Выбор средства программирования обосновывается тем, что Python является одним из самых удобных языков, предназначенных для работы с большим количеством данных. При максимальном количестве рассматриваемых логистических компаний 100 и количестве периодов 100 в результате проведения эксперимента (рис. 1) было выявлено число компаний, которые прекратят свою деятельность в определенный период времени, а также те, которые продолжат или вновь начнут свое функционирование в течение всего модельного времени.
Таким образом, выло выявлено, что система становится относительно устойчивой примерно на сороковом шаге. При этом существуют периоды, где количество логистических компаний, прекративших свою деятельность, увеличивается. Особенно это наблюдается в начальные периоды времени. В первой четверти временного промежутка система находится в наиболее неустойчивом состоянии. Прекращение деятельности компаний объясняется совокупностью естественных негативных факторов, поскольку дополнительных условий на модель не накладывалось.
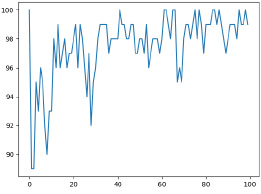
Рис. 1. Динамика изменения численности логистических компаний
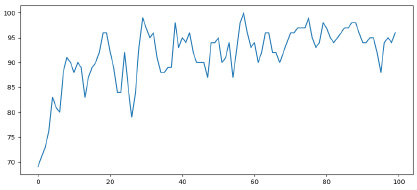
Рис. 2. Динамика изменения численности логистических компаний при наложении дополнительных негативных факторов
Если в модель ввести некоторое допущение, указав, дополнительные факторы (такие как ухудшение экономического состояния региона, сокращение численности квалифицированного персонала, появление новых контрагентов, обладающих высокотехнологическим оборудованием, с которыми сложно конкурировать традиционным компаниям и другие факторы), влияющие на поведение системы, то динамика изменения численности логистических компаний изменится. Так, например, будем на каждом шаге для матрицы взаимодействия M изменять случайно выбранный элемент, не стоящий на диагонали, на случайное число не из диапазона от -1 до 1, а из диапазона от -2 до 1. В таком случае количество компаний, прекративших свою деятельность, будет увеличиваться, однако, как видно на рисунке 2, система также окажется достаточно устойчивой к изменениям.
Заключение
Модель Соле-Манрубиа является современным средством описания эволюционной динамики. Построенная модификация модели учитывает стохастический характер происходящих процессов. Её использование удобно не только для анализа биологических систем, но также для анализа жизненного цикла сложных логистических систем. Учитывая нечеткие характеристики в формировании вектора, описывающего состояние системы в каждый момент времени, можно получить более достоверную картину, показывающую динамику системы.
В дальнейшем модель можно усовершенствовать, заменив в матрице взаимодействия случайные значения на случайные числа с треугольной функцией принадлежности, значения которой определяются интегральным показателем экономического состояния организации.
Работа выполнена в рамках темы ФНИР «Трансформация социокультурного пространства регионов Арктической зоны Российской Федерации в современных условиях» № государственной регистрации 122012100405-4.
Библиографическая ссылка
Кошуняева Н.В. МОДЕЛЬ СОЛЕ-МАНРУБИА С НЕЧЁТКИМИ ХАРАКТЕРИСТИКАМИ ДЛЯ ЛОГИСТИЧЕСКИХ КОМПАНИЙ // Вестник Алтайской академии экономики и права. 2022. № 4-2. С. 209-214;URL: https://vaael.ru/ru/article/view?id=2159 (дата обращения: 07.01.2026).
DOI: https://doi.org/10.17513/vaael.2159

