Введение
Модель Блэка-Скоулза-Мертона (BSM), разработанная в 1973 году Фишером Блэком, Робертом Мертоном и Майроном Скоулзом для определения цены опционных контрактов, все еще широко используется сегодня. Это считается одним из лучших способов определения справедливой цены опционов. Модель требует пяти входных переменных – цены исполнения опциона, текущей цены акций, времени до истечения срока действия, безрисковой ставки и волатильности базовой акции – для получения теоретической стоимости опциона. Единственным параметром в модели, который нельзя наблюдать напрямую, является волатильность базового актива (акции). На практике трейдеры обычно работают с так называемой подразумеваемой волатильностью. В этом подходе модели ценообразования опционов используются для преобразования наблюдаемых цен на производные финансовые инструменты в рыночный прогноз предполагаемой волатильности фиксированного будущего горизонта. Однако эти процедуры зависят от модели и дополнительно включают в показатель потенциально изменяющуюся во времени премию за риск волатильности; в результате они не дают объективного прогноза волатильности базового финансового актива.
В последние годы литература по волатильности выиграла от наличия высокочастотных финансовых данных (то есть наблюдений, отобранных на временном горизонте, меньшем, чем торговый день, например, 1 минута, 1 секунда или даже данные по тику за тиком). Совершенствование компьютерных технологий, а также системы записи и хранения данных сделали эти наборы данных легкодоступными для исследователей. В результате подход к измерению и моделированию волатильности значительно изменился. Был предложен новый подход, называемый Реализованной волатильностью, который использует информацию в высокочастотных данных. Этот подход оценивает волатильность путем суммирования квадратов внутридневной доходности, отобранных с очень короткими интервалами (высокие частоты). «Идея заключается в том, что если траектория выборки волатильности непрерывна, то увеличение частоты выборки дает произвольно точные оценки волатильности в любой данный момент времени» [1]. В этом подходе, волатильность становится наблюдаемой, применимы традиционные модели временных рядов и возможно многомерное моделирование.
Основное преимущество использования высокочастотных финансовых данных для оценки волатильности заключается в повышении качества прогноза волатильности. Было продемонстрировано, что высокочастотные данные улучшают нашу способность понимать и прогнозировать финансовую волатильность. В связи с этим недавняя работа по оценке, моделированию и прогнозированию волатильности и корреляции условной доходности основывалась на вышеуказанном преимуществе, чтобы предложить новые оценки реализованной волатильности (реализованные меры), «которые более эффективны, устойчивы к влиянию микроструктуры рынка и могут оценивать изменение из-за непрерывной части ценового процесса отдельно от изменения из-за «скачка» части ценового процесса» [2].
Хотя было задокументировано, что высокочастотные данные о ценах приводят к точному измерению и прогнозированию ненаблюдаемой волатильности активов, их полезность при ценообразовании производных финансовых инструментов не была полностью исследована. Была проделана небольшая работа по оценке эффективности высокочастотных оценщиков волатильности, например, при ценообразовании опционов. Существующие исследования в этой области были сосредоточены в основном на оценке эффективности различных моделей ценообразования опционов. В результате большинство исследований ограничено подмножествами реализованных оценок волатильности. Учитывая вышесказанное, целью данного исследования является оценка эффективности высокочастотных оценок волатильности при ценообразовании опционов. Цель исследования – определить реализованную оценку волатильности, которая дает наилучшую цену опциона. С этой целью мы оценили европейские опционы «колл» и «пут», используя недавно предложенные высокочастотные оценки волатильности, и сравнили прогнозируемую теоретическую цену/ модельную стоимость опционов с их рыночными ценами.
Остальная часть этой статьи организована следующим образом: Во втором разделе рассматривается существующая эмпирическая литература по проблеме, исследуемой в исследовании. В разделе 3 описываются данные и методы, использованные для исследования. В разделе результатов представлены и обсуждаются результаты исследования и делаются обоснованные выводы из них.
Обзор эмпирической литературы
Обзор предыдущих исследований о полезности оценщиков реализованной волатильности в ценообразовании опционов показывает, что большая часть существующей работы в этой области была сосредоточена главным образом на оценке эффективности моделей ценообразования опционов, а не самих оценщиков реализованной волатильности. В результате большинство этих исследований ограничивается анализом только подмножества реализованных оценок волатильности.
Джоу, Ван и Чиу [3] изучили эффективность ценообразования опционов вне выборки в моделях оценки опционов типа HAR, основанных на ежедневной реализованной волатильности, построенной на основе 5-минутных рядов доходности индекса S&P500 и нелинейной асимметричной модели GARCH (NGARCH). Авторы проанализировали ошибки оценки вне выборки в четырех моделях – модели ценообразования опционов log-HAR, HARG, предложенной Корси и др. (2010), модели ценообразования опционов NGARCH и модели BSM в качестве эталонной модели. Эмпирический анализ показал, что ошибки оценки вне выборки в моделях типа HAR ниже, чем в других моделях. Вывод заключался в том, что модели типа HAR успешно предсказывают цены опционов вне выборки, вероятно, потому, что они были основаны на реализованной волатильности.
Корси, Фузари и Ла Веккья [4] разработали модель ценообразования опционов со стохастической волатильностью в дискретном времени, которая использует историческую информацию, содержащуюся в высокочастотных данных. Они использовали показатель реализованной волатильности (RV), называемый непрерывной реализованной волатильностью (CRV), который оценивает непрерывную составляющую RV. Их анализ опционов на индекса S&P500 показывает, что Гетерогенная авторегрессионная гамма с кредитным плечом (HARGL) модель превзошла другие модели в исследовании благодаря использованию непрерывной оценки реализованной волатильности и высокой стойкости и сглаживанию, генерируемым спецификацией модели волатильности “HARGL”.
Стентофт [5] использовал обратную гауссову модель с 30-минутным показателем доходности RV для определения цен на опционы по трем отдельным акциям. Исследование показывает, что реализованная волатильность уменьшает ошибки ценообразования опционов на акции.
Кристофферсен, Фоуну, Джейкобс и Меддахи [6] исследовали добавленную экономическую стоимость, связанную с улучшением показателей прогнозирования оценщиков реализованной волатильности. Они использовали модель с дискретным временем, которая позволяет проводить оценку опционов в закрытой форме. Динамика волатильности модели состояла из двух компонентов – компонента GARCH и компонента реализованной волатильности. Исследование показало, что включение реализованной волатильности значительно снижает ошибки ценообразования эталонной модели по уровням денежности, зрелости и волатильности.
Тонг и Хуан [7] изучили роль реализованной волатильности в ценообразовании опционов на индекс волатильности (VIX). Авторы использовали обобщенную аффинную модель реализованной волатильности (GARV) Кристофферсена и др. (2014) и реализованную обобщенную авторегрессионную условно гетероскедастическую модель (GARCH) Хансена и Хуанга (2016) и Хансена и др. (2012) для моделирования совместной динамики базового индекса S& P500 (SPX) и реализованной волатильности. В исследовании использовалось реализованное ядро, предложенное Барндорфом‐Нильсеном и др. (2008) для оценки реализованной волатильности. Авторы обнаружили, что модели с реализованной волатильностью значительно превосходят конкурирующие модели, основанные только на ежедневной доходности, как в выборке, так и вне ее. В частности, реализованная модель GARCH обеспечила наилучшие цены на опционы.
Хуан, Тонг и Ван [8] также использовали гетерогенную авторегрессионную гамму с расширенным кредитным плечом (LHARG) с реализованной волатильностью для определения цены фьючерсов на VIX. Они обнаружили, что реализованная волатильность значительно улучшает ценовые характеристики модели.
Убуката и Ватанабе [9] проанализировали эффективность моделей ARFIMA(X) и HAR(X) с ежедневной реализованной волатильностью и моделей ARCH с ежедневной доходностью при ценообразовании опционов на фондовые индексы Nikkei 225. Реализованные меры, использованные в исследовании, включали реализованную волатильность со специальными и оптимальными частотами выборки, двухмасштабные оценки Чжана и др. (2005), Банди и Рассела (2011) и реализованные оценки ядра (плоская вершина) Барндорфа-Нильсена и др. (2004), Барндорфа-Нильсена и др. (2008). Авторы использовали авторегрессионную дробно интегрированную скользящую среднюю (ARFIMA) и гетерогенную интервальную авторегрессионную (HAR) модель Корси и (2009) для моделирования динамики реализованной волатильности. Для моделей типа ARCH они использовали простую модель GARCH, предложенную Боллерслевым (1986), модель EGARCH (экспоненциальная модель GARCH) Нельсона (1991), которая может отражать асимметрию волатильности, и модель FIEGARCH (фракционно интегрированная модель EGARCH) Боллерслева и Миккельсена (1996), которая также может учитывать свойство волатильности с длительной памятью. Цены их опционов были рассчитаны в соответствии с допущениями нейтральности к риску и нейтральности без риска (то есть с использованием метода Дуана 1995). Исследование показало, что модель ARFIMAX с ежедневной реализованной волатильностью работает лучше всего.
Наконец, Такеучи-Ногимор [10] проанализировал производительность реализованных моделей GARCH на основе реализованных ядер, предложенных Бардорфф-Нильсеном и др. и реализовал волатильность с помощью экспоненциального GARCH (EGARCH) и моделей Блэка–Шоулза в ценообразовании опционов. Основываясь на среднеквадратичной ошибке результатов оценки, исследование показало, что реализованные модели GARCH работают лучше, чем другие модели в исследовании. Кроме того, было установлено, что реализованные модели GARCH с реализованными ядрами (без неторговых часовых доходностей) превосходили реализованные модели GARCH только с реализованной волатильностью.
Материалы и методы исследования
Для целей этого исследования мы загружали цепочки опционов для корпорации Microsoft, корпорации Bank of America и компании Coca-Cola в конце каждого торгового дня (16:00) из Yahoo Finance. Период выборки для цепочек опционов охватывал 2021.08.02–2021.09.02. Мы также получили исторические данные о ценах закрытия (данные за 5 минут) для вышеуказанных акций за период 2020.02.06–2021.09.02 от Finam. Наконец, мы получили информацию о безрисковой ставке (данные о ежедневных ставках казначейских векселей) от Министерства финансов США.
Для оценки волатильности акций, лежащих в основе опционных контрактов, в этом исследовании использовались самые последние высокочастотные оценки волатильности (реализованные меры), доступные в литературе по волатильности. Ниже представлено краткое описание реализованных оценок волатильности, использованных для исследования:
1) Реализованная дисперсия/Реализованная волатильность (rRVar): Эта оценка вычисляет ежедневную Реализованную дисперсию. Реализованная дисперсия или реализованная волатильность (RV) – это сумма квадратов внутридневной доходности.
2) Реализованные ковариации с помощью усреднения по подвыборке (rAVGCov): Оценщик rAVGCov вычисляет реализованные отклонения путем усреднения RV по частично перекрывающимся сеткам. Он был впервые представлен Чжаном и др [11].
3) Модулированная реализованная ковариация (rMRCov): Модулированная реализованная ковариация вычисляет одномерную или многомерную предварительно усредненную оценку Хауча и Подольского [12].
4) Оценка ковариации в двухкратном масштабе (rTSCov): Она вычисляет матрицу ковариации в двухкратном масштабе, предложенную в Чжаном и др. [11] и Чжан [13].
5) Надежная оценка ковариации в двух временных масштабах (rRTSCov): Она вычисляет надежную матрицу ковариации в двух временных масштабах, предложенную в Боудт и Чжан [14].
6) Реализованный оценщик ядра (rKernelCov): Он вычисляет реализованную ковариацию с использованием оценки ядра. Типы доступных ядер: Прямоугольное, Бартлетта, Второго порядка, Епанечникова, Кубическое, Пятое, Шестое, Седьмое, Восьмое, Парцен, Тьюки Хэннинг и модифицированное Тьюки Хэннинг. Для этого исследования мы использовали оценки ядра Епанечникова, Парцена и модифицированного ядра Туки Ханнинга.
7) Реализованная ковариация двух мощностей (rBPCov): Вычисляется реализованная ковариация двух мощностей (RBPCOV), определенная в Барндорф-Нильсен и Шепард [15].
8) Минимальная реализованная дисперсия (rMinRV): Вычисляется rMinRVar, определенный в Андерсен и другие [16].
9) Медианная реализованная дисперсия (rMedRV): Она вычисляет rMedRVar, определенный в Андерсен и другие [16].
10) Пороговая ковариация (rThresholdCov): Вычисляется матрица пороговой ковариации, предложенная в Гобби и Манчини [17].
11) Ковариация Хаяси-Йошиды (rHYCov): Вычисляется оценка ковариации Хаяси-Йошиды[18].
12) Реализованная ковариация, взвешенная по дальности (rOWCov): Она вычисляет Реализованную ковариацию, взвешенную по дальности (rOWCov), определенную в Boudt et al. [19].
13) Реализованная полуразность высокочастотного обратного ряда (rSV): Он вычисляет реализованные полуразности, определенные в Барндорф-Нильсен и др. [20]. В этом исследовании мы оценили как реализованную полувариантную обратную сторону, так и полувариантную обратную сторону.
14) Реализованная дисперсия на основе диапазона (RRV): Вычисляется оценка на основе реализованного диапазона, предложенная Кристенсеном и Подольским [21]. Для этой оценки мы выбрали M_k=10 и λ=0,7. M_k – длина блока, т.е. Количество высокочастотных возвратов в каждом неперекрывающемся блоке (K), а λ – коэффициент дисперсии. Обратите внимание, что M_k=10 и λ=0,7 для умеренно ликвидных активов.
15) Реализованная дисперсия на основе квантилей (QRV): Он вычисляет реализованную дисперсию на основе квантилей, разработанную Кристенсеном, Ооменом и Подольским [22]. Для этой оценки мы выбрали следующие гиперпараметры на основе рекомендаций, приведенных в Кристенсен и другие [22]: i) Mk = 40, λ = (0.9, 0.93, 0.95) и α = (0.3, 0.3, 0.4) ii) Mk = 20, λ = (0.8, 0.85, 0.95) и α = (0.1, 0.2, 0.3, 0.3) где Mk – длина блока, λ – квантили доходности и α – вес квантиля. Это дало нам две оценки в рамках этого подхода – Квантильная реализованная дисперсия (QRV) и модифицированная квантильная реализованная дисперсия (mQRV).
Для удобства представления в табличной форме мы сократили приведенные выше оценки волатильности следующим образом:
• Реализованные меры – RV, AV, MRC, TS, RTS, Epa, Par, mTH, BP, MiRV, MeRV, Thr, HY, OW, SV.do, SV.up, RRV, QRV, mQRV.
Модели для прогнозирования реализованной волатильности
Для целей прогнозирования реализованной волатильности в исследовании использовалась Гетерогенная авторегрессионная модель реализованной дисперсии –модель HAR-RV. Модель HAR-RV, предложенная Корси [23], представляет собой прогностическую модель для ежедневной интегрированной волатильности. Он прогнозирует будущую волатильность, используя ежедневный, еженедельный и ежемесячный компоненты. Модель основана на гипотезе гетерогенного рынка, которая означает, что агенты не идентичны. Из-за этой неоднородности реакция на новости может быть разной и, следовательно, вызывать разные компоненты волатильности. Модель HAR-RV предполагает, что волатильность может быть представлена как сумма волатильности, создаваемых определенными группами участников рынка, каждая из которых имеет разные временные границы. Динамика модели задается с помощью:
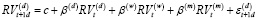
где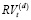 
– это реализованные волатильности за день t ,
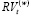– это средняя реализованная волатильность за последнюю неделю (последние 5 торговых дней), рассчитанная следующим образом:
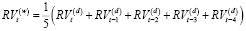
и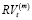 
– это средняя реализованная волатильность за последний месяц (последние 22 торговых дня), рассчитанная следующим образом:
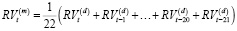
Модель HAR оценивается методом обычных наименьших квадратов в предположении, что в момент времени t условное среднее значение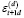 
равно нулю.
Для нашего исследования мы использовали модель HAR-RV со следующими характеристиками:
• Type: HAR,
• Lags: 1 5 22,
• Window Type: “rolling”
• Maximum lags 22
Мы использовали 5-минутные ряды доходности (30, 808 5-минутных доходностей) за период 2020.02.06–2021.09.02 для прогнозирования волатильности акций, лежащих в основе цепочек опционов в рамках модели HAR-RV. Мы придерживались мнения, что практически вся информация из высокочастотных данных содержится в 5-минутных данных, поэтому было принято решение оценить и спрогнозировать волатильность акций с использованием частоты выборки 5 минут. Другие работы, рассмотренные при выборе модели для исследования, включали Родионов и др. [24], Русская и др. [25], Зайцев [26], Зайцев и др. [27].
Модели Ценообразования Опционов
С момента разработки модели Блэка-Шоулза-Мертона (BSM) в 1973 году для ценообразования опционных контрактов было предложено множество альтернативных моделей ценообразования опционов. Однако BSM по-прежнему широко используется сегодня; он считается одним из лучших способов определения справедливой цены опционов. В связи с этим в данном исследовании мы использовали формулы BSM для цен европейских опционов «колл» и «пут» при ценообразовании опционных контрактов. Эти формулы являются следующие [28]:
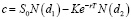
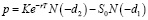
где
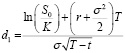
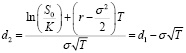
В приведенных выше формулах c и p представляют цены европейских опционов «колл» и «пут» в момент времени t соответственно, T – дата погашения опцион, S0 –текущая цена акций, K – цена исполнения, σ – волатильность базовой акции, r – непрерывно увеличивающаяся безрисковая ставка в год, а функция N(x) – функция распределения совокупной вероятности для переменной со стандартным нормальным распределением.
Оценка прогноза Волатильности
Успех оценщиков волатильности зависит от их эффективности прогнозирования вне выборки. На практике различные функции потерь могут использоваться для измерения эффективности различных прогнозов волатильности. Можно было бы использовать как статистические, так и экономические показатели. Это исследование направлено на определение высокочастотной оценки волатильности, которая дает наилучшую цену опциона. В связи с этим мы оценили точность прогнозов волатильности, сравнив прогнозируемую теоретическую цену/модельную стоимость опциона с рыночной ценой. Ниже приводится описание конкретных шагов, связанных с нашей методологией оценки:
1) Прогнозируйте волатильность акций, лежащих в основе цепочек опционов, используя высокочастотные оценки волатильности, указанные выше. Даты прогноза: 2021.08.02–2021.09.02. Обратите внимание! В данном периоде мы использовали только торговые дни.
2) Рассчитайте цену опционов на акции по модели Блэка-Шолеса-Мертона на даты ценообразования опционов (2021.08.02–2021.09.02) на основе оценки / прогнозов высокочастотной волатильности на шаге (1). Обратите внимание! Мы выбрали все опционы “колл” и «пут», для которых цена акций на дату определения цены опциона была на 10 долларов выше или ниже цены исполнения, т. е. мы использовали только опционы, близкие к «на деньги» (ATM). Это было сделано для обеспечения целесообразности использования модели Блэка-Шолеса-Мертона и минимизации эффекта волатильности, поскольку модель Блэка-Шолеса-Мертона предполагает, что волатильность постоянна.
3) Сравните прогнозируемую теоретическую цену / значение модели Блэка-Шолеса-Мертона для опционов с их рыночными ценами и рассчитайте среднюю абсолютную ошибку (MAE) на каждую дату ценообразования и определите оценку волатильности или оценки, которые имеют минимальную среднюю ошибку на каждый день. Обратите внимание! Для сравнения мы использовали запрашиваемую цену опциона.
4) Определите общее количество раз, когда каждая оценка волатильности была предпочтительной оценкой (т.е. оценкой минимальной средней ошибки) в течение периодов ценообразования (2021.08.02–2021.09.02). Оценка волатильности, которая является предпочтительной в большинстве случаев, т. е. оценка волатильности, которая имеет самую высокую частоту с точки зрения функций потерь MAE, считается лучшей оценкой.
Результаты исследования и их обсуждение
В этом исследовании оценивались девятнадцать (19) высокочастотных оценщиков волатильности при оценке опционов «колл» и «пут» на акции Bank of America, Coca-Cola и Microsoft в течение 24 торговых дней (02.08.2021–02.09.2021) путем сравнения прогнозируемой теоретической цены (модельной стоимости) опционов с их рыночными ценами (цена запроса). В дальнейшем мы обобщаем результаты, полученные в этом отношении, и делаем из них обоснованные выводы.
Опционы «Колл» и «Пут» – Bank of America (BAC)
В таблице 1 ниже представлены результаты высокочастотных оценок волатильности при оценке опционов «колл» и «пут» на акции Bank of America. Результаты показывают, сколько раз (дней) каждая оценка волатильности была предпочтительной оценкой на основе критерия оценки средней абсолютной ошибки.
Результаты оценки, приведенные в таблицах 1 выше, показывают, что для опционов «колл» на акции Bank of America лучшей оценкой волатильности была реализованная оценка ковариации (BP), поскольку она была предпочтительной 4 раза из 24 торговых дней. После двухуровневой реализованной дисперсии были оценки минимальной реализованной дисперсии (MiRV) и реализованной дисперсии на основе диапазона (RRV), которые были предпочтительнее по 3 раза каждый. Таблица 1 также показывает, что для опционов «пут» на акции Bank of America предпочтительной оценкой волатильности были оценки реализованного ядра (Epa, Par, mTH). Эти оценки были предпочтительнее 10 раз каждый из 24 торговых дней. Опять же, в непосредственной близости от оценщиков ядра находилась оценка реализованной дисперсии на основе диапазона (RRV), которая была предпочтительнее 8 раз.
Таблица 1
Количество дней, в течение которых предпочтение отдавалось каждой оценке волатильности: BAC
|
Оценщики волатильности |
Количество предпочтительных дней_«Колл» |
Количество предпочтительных дней_«Пут» |
|
RV |
2 |
3 |
|
AV |
2 |
1 |
|
MRC |
0 |
0 |
|
TS |
1 |
0 |
|
RTS |
0 |
0 |
|
Epa |
1 |
10 |
|
Par |
1 |
10 |
|
mTH |
1 |
10 |
|
BP |
4 |
0 |
|
MiRV |
3 |
0 |
|
MeRV |
2 |
0 |
|
Thr |
1 |
0 |
|
HY |
0 |
0 |
|
OW |
0 |
0 |
|
SV.do |
0 |
0 |
|
SV.up |
2 |
0 |
|
RRV |
3 |
8 |
|
QRV |
2 |
0 |
|
mQRV |
1 |
2 |
Таблица 2
Количество дней, в течение которых предпочтение отдавалось каждой оценке волатильности: KO
|
Оценщики волатильности |
Количество предпочтительных дней_«Колл» |
Количество предпочтительных дней_«Пут» |
|
RV |
2 |
2 |
|
AV |
0 |
3 |
|
MRC |
0 |
0 |
|
TS |
1 |
1 |
|
RTS |
0 |
0 |
|
Epa |
0 |
3 |
|
Par |
0 |
3 |
|
mTH |
0 |
3 |
|
BP |
4 |
3 |
|
MiRV |
2 |
1 |
|
MeRV |
1 |
1 |
|
Thr |
0 |
2 |
|
HY |
1 |
3 |
|
OW |
0 |
0 |
|
SV.do |
0 |
0 |
|
SV.up |
1 |
0 |
|
RRV |
3 |
3 |
|
QRV |
6 |
1 |
|
mQRV |
3 |
1 |
Опционы «Колл» и «Пут»– Coca-Cola (KO)
В таблице 2 ниже приведены результаты оценки высокочастотной волатильности при оценке опционов «колл» и «пут» на акции Coca-cola. Результаты показывают, сколько раз (дней) каждая оценка волатильности была предпочтительной оценкой на основе критерия оценки средней абсолютной ошибки.
Как показано в таблице 2 выше, для опционов «колл» на акции Coca-Cola наилучшей оценкой волатильности с точки зрения критерия оценки средней абсолютной ошибки оказалась реализованная дисперсия на основе квантилей (QRV). Эта оценка была предпочтительной шесть (6) раз из 24 торговых дней. После оценки реализованной дисперсии на основе квантилей следует реализованная двунаправленная ковариация (BP), которая была предпочтительнее 4 раз. Для опционов «пут» на акции Coca-Cola лучшими оценками волатильности оказались реализованные оценки ядра (Epa, Par, mTH), Реализованные ковариации с помощью усреднения по подвыборке (AV), Реализованная ковариация с двумя степенями (BP), ковариация Хаяси-Йошиды (HY) и Реализованная дисперсия на основе диапазона (RRV). Каждому из них отдавали предпочтение по 3 раза
Опционы «Колл» и «Пут»– Microsoft (MSFT)
В таблице 3 ниже приведены результаты, полученные при оценке опционов «колл» и «пут» на акции Microsoft, основанные на оценках высокочастотной волатильности
Из таблицы 3 выше видно, что для колл-опционов на акции Microsoft лучшей оценкой волатильности была оценка ковариации в двухкратном масштабе (TS), которая была предпочтительнее 4 раза из 24 торговых дней. Для опционов на покупку акций Microsoft наиболее эффективными оценщиками с точки зрения средней абсолютной потери ошибок были Реализованные оценки ядра (Epa, Par, mTH) и оценка реализованной дисперсии (RV). Каждый из них был предпочтительнее 5 раз из 24 торговых дней. В непосредственной близости от оценок ядра и реализованной дисперсии находилась медиана реализованной дисперсии (MeRV), которые оба были предпочтительнее в 4 раза.
Таблица 3
Количество дней, в течение которых предпочтение отдавалось каждой оценке волатильности: MSFT
|
Оценщики волатильности |
Количество предпочтительных дней _«Колл» |
Количество предпочтительных дней _«Пут» |
|
RV |
3 |
5 |
|
AV |
2 |
1 |
|
MRC |
0 |
0 |
|
TS |
4 |
0 |
|
RTS |
0 |
1 |
|
Epa |
2 |
5 |
|
Par |
2 |
5 |
|
mTH |
2 |
5 |
|
BP |
0 |
2 |
|
MiRV |
1 |
0 |
|
MeRV |
0 |
4 |
|
Thr |
2 |
1 |
|
HY |
1 |
0 |
|
OW |
0 |
1 |
|
SV.do |
1 |
0 |
|
SV.up |
3 |
1 |
|
RRV |
0 |
2 |
|
QRV |
3 |
1 |
|
mQRV |
2 |
0 |
Выводы
В этом исследовании оценивалась эффективность высокочастотных оценщиков волатильности при оценке опционов «колл» и «пут» на акции Bank of America, Coca-Cola и Microsoft. С этой целью мы оценили и сравнили прогнозируемую теоретическую стоимость опционов, рассчитанную на основе оценки/прогноза высокочастотной волатильности, с рыночной ценой (ценой предложения) опционов. Выводы, представленные в предыдущем разделе, показали, что
1) для опционов «колл» на акции Bank of America лучшей оценкой волатильности была оценка реализованной дисперсии (BP). Это было предпочтительнее 4 раза из 24 торговых дней,
2) для опционов «пут» на акции Bank of America предпочтительной оценкой волатильности были оценки реализованного ядра (Epa, Par, mTH). Эти оценки были предпочтительнее 10 раз каждый из 24 торговых дней,
3) для колл-опционов на акции Coca-Cola лучшей оценкой волатильности оказалась реализованная дисперсия на основе квантилей (QRV). Эта оценка была предпочтительной шесть (6) раз из 24 торговых дней,
4) для опционов «пут» на акции Coca-Cola лучшими оценками волатильности оказались реализованные оценки ядра (Epa, Par, MTH), Реализованные ковариации с помощью усреднения по подвыборке (AV), Реализованная ковариация с двумя степенями (BP), ковариация Хаяси-Йошиды (HY) и Реализованная дисперсия на основе диапазона (RRV). Каждый из них был предпочтительнее 3 раза,
5) для опционов на покупку акций Microsoft лучшей оценкой волатильности была оценка ковариации в двух временных масштабах (TS), которая была предпочтительнее 4 раза из 24 торговых дней,
6) для опционов на покупку акций Microsoft наиболее эффективными оценщиками с точки зрения средней абсолютной потери ошибок были оценки реализованного ядра (Epa, Par, mTH) и оценка реализованной дисперсии (RV). Каждый из них был предпочтительнее 5 раз из 24 торговых дней.
В свете вышеизложенных выводов делается вывод о том, что, хотя ни одна из оценок волатильности не является предпочтительной все время с точки зрения функции потери средней абсолютной ошибки, реализованная оценка ядра (Epa, Par, mTH) превосходит другие конкурирующие оценки волатильности при оценке опционов на акции Bank of America, Coca-Cola и Microsoft.
Библиографическая ссылка
Гайомей Д. ВЫСОКОЧАСТОТНАЯ ОЦЕНКА ВОЛАТИЛЬНОСТИ И ЦЕНА ОПЦИОНА // Вестник Алтайской академии экономики и права. – 2022. – № 4-2. – С. 167-176;URL: https://vaael.ru/ru/article/view?id=2153 (дата обращения: 18.04.2024).