Научный журнал

Вестник Алтайской академии экономики и права

Print ISSN 1818-4057

Online ISSN 2226-3977

Перечень ВАК

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Шульженко А.О. 1

---

1 ФГБОУ ВО «Санкт-Петербургский государственный университет»

В статье представлены разработки в части предиктивного управления логистической инфраструктурой в макрологистических системах в условиях высокой турбулентности внешней экономической среды, определяемой ужесточением санкционного режима, глобальным замедлением и потенциальной переориентацией внешнеэкономических связей. Глобальное и слабопрогнозируемое изменение параметров потоков внешнеторговых грузов требует применения аппарата адаптивного управления логистической инфраструктурой макроуровня, разработка которого выполнена с использованием математического обеспечения реализации методов машинного обучения, основанных на положениях байесовского подхода. В частности, представленные в статье результаты детального анализа априорных распределений по параметрам моделей с последующим их байесовским сравнением, а также сопряженных апостериорных распределений параметров исследуемых процессов позволяют разрабатывать решения по определению приоритетных направлений ускоренного развития макрологистической инфраструктуры с учетом колебаний основных факторов.

Статья в формате PDF

474 KB

логистическая инфраструктура

транспортно-логистические процессы

машинное обучение в логистике

байесовский подход

1. Прокофьева Т.А., Гончаренко С.С. Управление развитием логистической инфраструктуры – стратегическое направление реализации транзитного потенциала России в системе евроазиатских МТК и интенсивного экономического роста регионов европейского севера, Сибири и Дальнего Востока // Вестник транспорта. 2019. № 6. С.8-15.

2. Савин Г.В. Логистическая стратегия в обеспечении потоков транспортно-логистической системы мезо-уровня // Российский экономический вестник. 2019. № 5. С. 166-171.

3. Шульженко Т.Г., Молонова А.В., Новицкая В.Д. Формирование предиктивных аналитических моделей развития логистической инфраструктуры // Актуальные проблемы развития экономики и менеджмента. 2020. № 3. С. 145-155.

4. Шульженко Т.Г. Совершенствование методов стратегического анализа в задачах инновационного развития логистической инфраструктуры / РИСК: Ресурсы. Информация. Снабжение. Конкуренция. 2020. № 2. С. 21-29.

5. Aggarwal, C. C. Linear Algebra and Optimization for Machine Learning. Springer. 2020.

6. Barzilai J., Borwein J.M. Two-Point Step Size Gradient Methods. IMA Journal of Numerical Analysis. 1988. № 8(1). Р. 141–148.

7. Blei D.M., Smyth P. Science and data science. In: Proc. Natl. Acad. Sci. U. S. A. 2017.

8. Blyde J., Molina D. Logistic Infrastructure and international location of fragmented production. Journal of International Economics. 2015. № 95. Р. 319-332.

9. Carlin B.P., Louis T.A. Bayesian Methods for Data Analysis, Third Edition. Boca Raton, FL: Chapman and Hall/CRC, 2008.

10. Domingos P. The Master Algorithm, Basic Books, 2015.

11. Fletcher R. On the Barzilai–Borwein Method. In: Qi L., Teo K., Yang X. (eds.). Optimization and Control with Applications. Applied Optimization 96, Р. 235–256. Boston: Springer, 2005.

12. Franceschi L., Donini M., Frasconi P., Pontil M. Forward and Reverse Gradient-Based Hyperparameter Optimization. ICML, 2017.

13. Gelman A., Carpenter B. Bayesian analysis of tests with unknown specificity and sensitivity. MedRxiv, 2020.

14. Kevin P.M. Probabilistic Machine Learning: An Introduction, MIT Press, 2021.

15. Tibshirani R. Regression Shrinkage and Selection via the lasso. Journal of the Royal Statistical Society. Series B (methodological). 1996. № 58(1). Р. 267–288.

Введение

В настоящее время производственные и производственно-коммерческие системы под влиянием действующих экономических и политических факторов демонстрируют высокую уязвимость как при участии в глобальных экономических процессах, так и при организации деятельности во внутренней экономике. Задача сохранения устойчивости и конкурентоспособности в турбулентной экономической среде определяет необходимость поддержания эффективности выполнения вспомогательных процессов, в частности, транспортно-логистических. Вместе с тем, проявление негативного влияния агрессивной внешней среды требует значительных изменений в конфигурациях сложившихся систем доставки, однако реализация указанного требования сдерживается степенью готовности макрологистической инфраструктуры страны к резкому изменению параметров грузопотоков, в частности, их переориентации на юго-восточное направление, потенциальному наращиванию интенсивности внутристрановы́х грузопотоков, а также грузопотоков в рамках Евразийского экономического союза. Таким образом, актуализируется целый ряд проблем, требующих скорейшего решения – в частности, разработки механизмов адаптивного управления материальными потоками в макрологистической системе с учетом имеющихся ограничений на пропускную способность логистической инфраструктуры, выявления приоритетных направлений инвестиций в ускоренное развитие пропускной способности логистической инфраструктуры макроуровня для сохранения устойчивого функционирования производственных и производственно-коммерческих систем и ряд других. Глобальная трансформация условий ведения экономической деятельности, внешней среды функционирования российских производственных и производственно-коммерческих систем, реализации процессов международной торговли, организации и выполнения транспортно-логистических процессов в макрологистических системах требует модернизации аппарата принятия и обоснования решений в рамках концепций предиктивного и адаптивного управления инфраструктурным обеспечением транспортно-логистических процессов.

Эффективность функционирования современных производственных систем, действующих в условиях сетевой экономики сервисного типа, в значительной степени определяется качеством организации вспомогательных процессов, к числу наиболее значимых из которых относятся транспортно-логистические процессы. Особое значение данная задача приобретает для международных производственных и производственно-коммерческих систем, вспомогательные процессы которых требуют наличия развитой логистической инфраструктуры. Между тем, обеспечение соответствующего потребностям производственной или производственно-коммерческой системы уровня развития логистической инфраструктуры сопряжено с существенными инвестициями, что, в свою очередь, приводит к потере финансовой устойчивости участников, росту логистических издержек, а также дополнительным расходам государственного бюджета, поскольку формирование логистической инфраструктуры для обслуживания международных систем входит сегодня в число приоритетных задач государственной политики.

Вопросы, связанные с инфраструктурным обеспечением вспомогательных процессов международных производственных систем, нашли достаточно широкое освещение в современных научных источниках. В частности, в работах [2, 3, 8] рассматриваются методы реализации принципов логистического управления инфраструктурным обеспечением функционирования международных производственных и производственно-распределительных систем. Проблематика государственного управления развитием макрологистической инфраструктуры также получила достаточное развитие в трудах российских и зарубежных ученых (например, [1]). Однако в представленных работах не исследуется уникальная ситуация, характеризуемая всеобщим изменением параметров грузопотоков в логистических системах различных уровней, в которой в настоящее время выстраивают свою деятельность российские экономические субъекты. Вместе с тем, недостаточность обоснования решений по управлению макрологистической инфраструктурой в сложившихся условиях с учетом имеющихся ограничений по ее пропускной способности, по выбору рациональных направлений ее ускоренного развития выступает дополнительным фактором риска для российской экономической системы. Привлечение математического аппарата при обосновании решений по развитию и адаптивному управлению инфраструктурным обеспечением логистических процессов с учетом прогнозируемого изменения факторов внешней среды, обусловливающих потенциальную нагрузку на инфраструктурные объекты в перспективном периоде, является необходимым условием сохранения устойчивого функционирования российских производственных и производственно-коммерческих систем.

Целевая ориентированность экономики на производство продукции с высокой добавленной стоимостью позволяет принять величину контейнеропотока в качестве результирующего показателя с позиций организации логистических процессов, вспомогательных для международных производственных и производственно-коммерческих систем, и выбора параметров логистической инфраструктуры. Таким образом, показатели контейнеропотока выступают в качестве ведущих факторов, определяющих требования к логистической инфраструктуре. Тогда цель исследования состоит в формировании математического аппарата управления факторами инфраструктурного обеспечения, основанного на реализации методов машинного обучения, позволяющего формировать решения с учетом изменений внешней среды, целевых установок производственных и производственно-коммерческих систем, а также государственных интересов. Следует отметить, что указанный показатель, а также разработанный на его основе подход по управлению логистической инфраструктурой могут рассматриваться в качестве эталонных, подлежащих масштабированию на другие группы грузов.

Материалы и методы исследования

Начальный этап исследования связан с формированием исходной базы, состав которой формируют показатели-признаки, выступающие в качестве факторов, влияющих на показатели контейнеропотока в страново́й производственно-коммерческий системе.

Учитывая значительную размерность исходной базы, а также качество данных, в качестве необходимого этапа рекомендуется выполнять предварительную подготовку данных по следующему алгоритму:

1. Очистка базы, удаление пустых строк.

2. Восполнение пропущенных значений. В силу неоднородности выборок в каждом из столбцов пропуски заполнены методом k ближайших соседей (k = 5) с последующим усреднением значений. Более формально: пусть xi,j – пропущенное значение в столбце с номером i. Номер пропущенного значения в столбце – j.

Тогда воспользуемся следующим алгоритмом для восполнения пропущенного значения xi,j :

3. Формирование результирующего показателя: в качестве целевого показателя принята величина контейнеропотока в страново́й производственно-коммерческой системе.

4. Удаление из базы показателей, в которых число пропущенных значений больше трети от числа строк в базе. Удаление показателей «Rail containers transport (TEU)», «Maritime containers transport (TEU)», поскольку они участвовали в формировании результирующего показателя.

После этапа очистки и предобработки данных произведен корреляционный анализ факторов, с последующим построением матрицы корреляции, в которую вошло 20 признаков (их список представлен в практической части). Наше предположение состояло в том, что факторы, коэффициент корреляции между которыми по абсолютному значению превосходит 0.8, являются сильно коррелированными и не могут быть включены в выборку для дальнейшего рассмотрения. Исходя из этого некоторые факторы были удалены, и для последующего анализа оставлено 10 слабо коррелированных факторов.

Основной гипотезой работы выступило предположение о наличии полиномиальной зависимости между целевым показателем и выбранными факторами. Для восстановления полиномиальной зависимости предлагается использовать байесовский подход в решении регресионных задач.

Дадим небольшое напоминание о сути байесовского подхода: нас будет интересовать апостериорное распределение на параметрах модели (и гипотеза максимального правдоподобия). Для нашего частного случая – это апостериорное распределение на векторах коэффициентов модели и wML. Отметим, что по теореме Байеса, апостериорное распределение пропорционально произведению априорного распределения на правдоподобие модели:

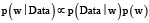(1)

Кроме этого, нас будет интересовать апостериорное распределение на исходах последующих экспериментов, которое получается маргинализацией распределения 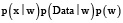по w:

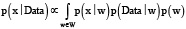(2)

где W – множество значений параметров (коэффициентов).

Получив апостериорное распределение на исходах, мы найдем максимальную апостериорную гипотезу; она и будет считаться реализацией новой точки данных.

Для дальнейшего построения регрессионной модели нам необходимо выбрать априорное распределение на параметрах модели, то есть зафиксировать p(w). В [15] показано, что, выбирая в качестве априорного распределения распределение Лапласа (двойное экспоненциальное) и умножая его на правдоподобие модели, которое вычисляется как

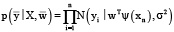(3)

где 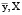– набор данных; 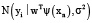– нормальное распределение с ожиданием 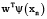и некоторой дисперсией σ2, мы получаем выражение для лассо-регрессии, то есть регрессии, которая минимизирует сумму квадратов отклонений (функция ошибки – сумма квадратов, так как сделано предположение о нормально распределенном шуме в данных) с регуляризационным членом 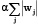, то есть L1 нормой вектора w.

Лассо-регрессия была выбрана нами не случайно, нашей целью было уменьшение числа ненулевых коэффициентов полинома, моделирующего зависимость между целевым показателем и факторами. Записывая лассо-регрессию в форме:

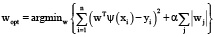(4)

получаем, что лассо-регрессия действительно увеличивает число нулевых элементов вектора коэффициентов. В двумерном случае это проиллюстрировано на рисунке 1.

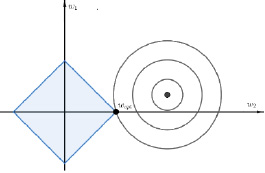
Рис. 1. Оптимальное значение w для случая лассо-регрессии

Строгое доказательство этого факта приведено в [15].

На следующем шаге исследования были выделены полиномиальные признаки, состоящие из полиномиальных комбинаций факторов степени, не превосходящей заданной нами константы. Иными словами, были получены все мономы xI, где 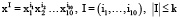, где через |I| обозначается мощность мультииндекса, то есть 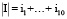. Далее, на основе этих значений построена модель лассо-регрессии, где в качестве обучающей выборки для модели взята часть базы исходных данных. Коэффициенты модели и явный вид полинома, описывающего зависимость между факторами и целевым показателем, также представлены в практической части.

Дальнейшее исследование связано с более глубоким изучением полученной зависимости. Одной из основных целей в работе являлось решение следующей задачи, которая на данном этапе может быть сформулирована аналитически: при получении новой точки данных то есть вектора 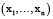мы хотим понять, какие параметры необходимо изменить, чтобы результирующий показатель изменился в большую сторону. Говоря конкретнее, пусть мы можем из менить каждый показатель на величину 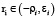, где 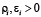. Задача состоит в том, чтобы найти такой набор ri, при которых 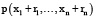было бы максимальным. Это ни что иное как задача поиска максимума функции на многообразии M, которое задается как 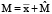, где .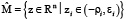

Известным способом решения этой задачи является метод множителей Лагранжа, который часто сложно реализовать для большого набора данных высокой размерности. Поэтому предлагается использовать итеративный процесс градиентного подъема из данной точки с условием (не)выхода за границы определенного выше многообразия. Опишем предложенный метод более детально в формате псевдокода:

Отметим, что выбор такого параметра γn не случаен. Авторы [9], [11] показали, что при таких значениях γn метод всегда сходится к локальному максимуму. Более того, представленный метод позволяет анализировать зависимости гораздо сложнее полиномиальных.

Представленный подход предлагается использовать в решении регрессионных задач, соответствующих задачам управления логистической инфраструктурой в международных производственно-коммерческих системах, а также логистической инфраструктурой макроуровня.

Результаты исследования и их обсуждение

Исходными данными для решения задачи приняты значения показателей (признаков), отражающие поведение факторов, влияющих на величину контейнеропотока. Всего в структуру базы исходных данных включены 88 признаков, укрупненно формирующих следующие группы: макроэкономические показатели, характеристики международной торговли, характеристики рыночных факторов (спроса/предложения), инвестиции в логистическую инфраструктуру. Значения по показателям подбирались по открытым статистическим базам (например, Всемирного банка, Всемирной торговой организации, Конференции ООН по торговле и развитию и других организаций). Общее количество точек (наблюдений) составило 2653 строки.

В результате выполненной предварительной очистки базы и удаления факторов с большим числом пропущенных значений была получен следующий набор показателей-факторов: ‘Rail containers transport (weight), Tonnes, Thousands’, ‘Maritime containers transport (weight), Tonnes, Thousands’, ‘Gross domestic product, constant prices’, ‘Gross domestic product, constant prices.1’, ‘Gross domestic product, current prices’, ‘Gross domestic product, current prices.1’, ‘Gross domestic product, current prices.2’, ‘Gross domestic product based on purchasing-power-parity (PPP) share of world total’, ‘Implied PPP conversion rate’, ‘Total investment’, ‘Volume of imports of goods and services’, ‘Volume of Imports of goods’, ‘Volume of exports of goods and services’, ‘Volume of exports of goods’, ‘Unemployment rate’, ‘Population’, ‘General government revenue’, ‘General government revenue.1’, ‘General government total expenditure’, ‘General government total expenditure.1’.

Результатом второго этапа очистки базы при удалении тесно коррелированных значений состав показателей-факторов сокращен до 10 (рис. 2).

Рассмотрим пример получения новой точки данных и проиллюстрируем работу алгоритма в этой ситуации (табл. 1).

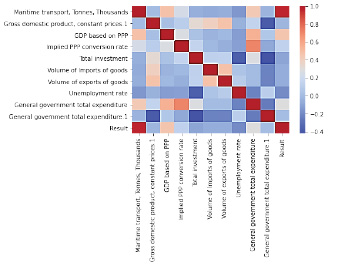
Рис. 2. Матрица корреляции признаков в финальной версии базы исходных данных

Явный вид полинома, полученного в результате обучения лассо-регрессии:

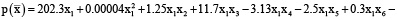
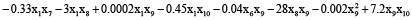(5)

Таблица 1

Набор данных

Таблица 2

Диапазоны допустимых изменений для каждого из параметров

Предсказание модели в этом случае составило 723542.5, в то время как реальное значение 766879 (погрешность составила 5%).

Тогда при постановке задачи увеличения величины контейнеропотока как показателя эффективности функционирования макрологистической инфраструктуры формулируем задачу максимизации целевого показателя на некотором многообразии, задаваемом ограничениями на координаты (табл. 2).

Далее применяя описанный выше метод градиентного спуска, получаем, что для максимизации целевого показателя нам необходимо разрабатывать комплекс мероприятий, нацеленных на сокращение значений показателей ‘Unemployment rate’, ‘General government total expenditure’, ‘Implied PPP conversion rate’ и увеличение показателей ‘Volume of exports of goods’, ‘Gross domestic product based on purchasing-power-parity (PPP) share of world total’.

С применением представленного подхода возможно решение обратной задачи: по изменениям показателей-факторов возможно предсказывать изменение результирующего показателя, следовательно, разрабатывать решения по адаптивному управлению логистической инфраструктурой вспомогательных процессов международных производственных (производственно-коммерческих) систем. Причем важно отметить, что подобные решения не всегда связаны с дополнительными инвестициями со стороны государства, например, при прогнозируемом росте величины контейнеропотока следует выполнить сопоставительный анализ прогнозных значений и степени использования потенциала имеющихся инфраструктурных мощностей (принципиальные положения для выполнения подобных оценок представлены в [4]).

Таблица 3

Наблюдаемые изменения параметров

Обращаясь к рассматриваемому примеру, следует отметить, что в процессе исследования выявлены изменения параметров модели (табл. 3), на основе которых построено прогнозное значение результирующего показателя, в целом демонстрирующее высокую точность относительно фактических значений. Между тем, отмечается некоторое временно́е отставание в формировании значений результирующего показателя, т.е. наличие временно́го лага.

С позиции принятия решений подобное поведение модели имеет определенные преимущества, поскольку формирует необходимые резервы времени для реализации разработанных мероприятий по управлению логистической инфраструктурой. Вместе с тем, направлением дальнейших исследований в части математического обеспечения решения подобных задач является изучение запаздывающих моделей.

Заключение

Выполненные разработки в части математического обеспечения реализации методов машинного обучения в управлении транспортно-логическими процессами производственных систем, основанные на положениях байесовского подхода, формируют необходимую основу для обоснования решений по адаптивному управлению инфраструктурными мощностями, обеспечивающими реализацию вспомогательных (логистических) процессов.

Перспективы развития представленного подхода связаны со следующими направлениями:

- расширение базы исходных данных, в том числе решение задачи формирования современного инструментария сбора и обработки данных с использованием цифровых технологий;

- выбор и исследование поведения результирующих показателей, отражающих различные аспекты функционирования производственных систем и систем логистического обеспечения, использования логистической инфраструктуры; разработка прикладных решений, ориентированных на принципы адаптивного управления производственными и логистическими системами;

- развитие математического аппарата, обеспечивающего оптимизацию рассматриваемых процессов, в частности, дальнейшее исследование моделей градиентного спуска, запаздывающих моделей.

Библиографическая ссылка