Введение
Невысокий уровень институционального развития российского фондового рынка имеет следствием не только его низкую капитализацию и ликвидность обращающихся на нем финансовых инструментов, но и высокие вход-выходные барьеры для новых игроков и трансакционные издержки операций с активами. Часто эти факторы оказывают решающее влияние на выбор вариантов инвестиций профессиональных и непрофессиональных участников рынка, в числе которых значительную долю составляют средние и крупные коммерческие банки, ставящие цель повысить доходность кредитно-инвестиционной деятельности и снизить риски на кратко- и среднесрочном интервалах.
Важным фактором выбора инвестиционной стратегии институционального (в значении профессионального) инвестора является ликвидность финансовых инструментов, включаемых в портфель, на «бытовом» уровне понимаемая как возможность обратной конвертации в наличные деньги в ограниченные сроки и без существенных (с позиции инвестора) потерь капитала. Именно по этой причине при формировании портфеля необходимо учитывать не только показатели доходности активов и риски вложений, но и уровень ликвидности портфеля в целом и отдельных активов в нем.
В работе авторы проводят сопоставительный анализ моделей Г. Марковица и У. Шарпа в приложении к задаче формирования оптимального портфеля финансовых активов институционального инвестора-агента развивающегося российского фондового рынка с учетом расширенного набора показателей качества активов, включающего наряду с доходностью и риском ликвидность ценной бумаги.
Далее: инвестиционный портфель – набор активов, собранных таким образом, чтобы доход от них соответствовал целям инвестора. Портфель может быть сформирован как с точки зрения сроков достижения цели, так и по составу инструментов. Идея формирования эффективного портфеля – корректного распределение риска и доходности.
Определение оптимального портфеля ценных бумаг представляет собой одну из задач, с которыми сталкиваются инвесторы на фондовом рынке. При выборе оптимального портфеля учитываются доходность и риск, как отдельных активов, так и портфеля в целом. При построении модели учтены корреляционные связи между доходностями активов.
Материалы и методы исследования
Методологическую основу работы составили:
- зарубежных и отечественных «классиков» портфельной теории, в том числе Г. Марковица [1, 2], Дж. Милнора [3], Н. Истерфурда [4], В. Шарпа [5], Ю. Тобина [6, 7], Р. Брейли и С. Майерса [8], Л. Дж. Гитмана [9], отечественных ученых и специалистов-практиков фондового рынка [10, 11, 12, 13, 14, 15, 16, 17, 18, 19], а также работы последнего времени преподавателей Российского экономического университета им. Г.В. Плеханова (М.А. Халикова, А.М. Антиколь, Д.А. Максимова, М.А. Горского, А.Ф. Грибова и др. [20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33];
- публикации российских ученых в области портфельного инвестирования, включая постановки и математические модели задач управления портфелем финансовых активов в статичном и динамическом вариантах [19, 23, 24, 27, 29, 30, 32, 34, 35];
- монографии и диссертационные исследования по проблемам институциональной экономики и финансовой деятельности [11, 12].
Статистическая и информационная база исследования сформирована на основе данных официальных интернет-сайтов: cbr.ru, banki.ru, raiffeisen.ru [36-46].
Объект исследования – портфель рисковых финансовых активов коммерческого банка, выступающего на фондовом рынке в роли институционального инвестора умеренно-агрессивного типа.
Предмет исследования – показатели, структура и состав портфеля рисковых финансовых активов коммерческого банка.
Цель исследования – сопоставительный анализ инструментария моделей Г. Марковица и У. Шарпа в приложении к задаче формирования оптимального портфеля финансовых активов институционального инвестора-агента развивающегося российского фондового рынка с учетом расширенного набора показателей качества активов, включающего наряду с доходностью и риском ликвидность ценной бумаги.
Результаты исследования и их обсуждение
Ниже рассматриваются модели оптимальных портфелей в постановках Г. Марковица и В. Шарпа для группы умеренно-агрессивных инвесторов (преобладающая группа инвесторов – непрофессиональных участников российского фондового рынка, в составе которой основная доля – инвестиционные фонды и коммерческие банки), ориентирующиеся на долгосрочные вложения и устойчивый рост инвестиционного капитала) с учетом дополнительного критерия ликвидности. Для указанной категории инвесторов допускается наличие в портфеле ценных бумаг среднего уровня риска. Основными инструментами инвестирования являются ценные бумаги крупных и средних, но надежных и длительно работающих на рынке компаний. Также в портфеле умеренно-агрессивного инвестора может присутствовать незначительная доля государственных ценных бумаг.
В перечень ценных бумаг для формирования портфеля на 21 сентября 2021 г. включены ценные бумаги, входящие в базу расчета индекса РТС, взвешенного по рыночной капитализации (free-float), композитные индексы российского фондового рынка, включающие наиболее ликвидные акции крупнейших и динамично развивающихся российских эмитентов, виды экономической деятельности которых относятся к основным секторам экономики. Каждой ценной бумаге был присвоен номер группы ликвидности в зависимости от среднего значения ликвидности данного актива (рисунки 1 и 2).
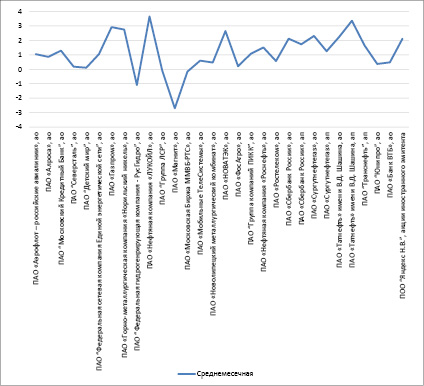
Рис. 1. Перечень ценных бумаг для формирования опорного портфеля инвестора умеренно-агрессивного типа [43]
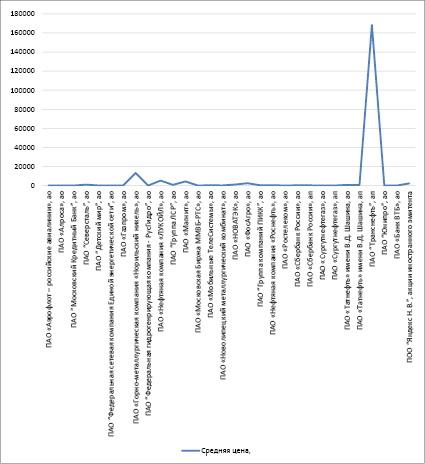
Риc. 2. Средняя цена ценных бумаг, выбранных для формирования опорного портфеля инвестора умеренно-агрессивного типа [43]
1. Структура и характеристика оптимальных портфелей, построенных по моделям Г. Марковица и В. Шарпа для инвестора с бюджетом до 500 тыс. руб.
Приведем модель оптимального инвестиционного портфеля Г. Марковица с критерием на максимум среднемесячной доходности и ограничением по ликвидности.
Ниже при описании модели (1) Г. Марковица будем использовать следующие обозначения переменных и параметров: i, j – акции из пула финансовых инструментов инвестора; xi – количество акций i-го эмитента в портфеле (целое положительное число); M – бюджет инвестора; 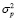 – уровень риска (волатильности) портфеля за период владения ценными бумагами;
– уровень риска (волатильности) портфеля за период владения ценными бумагами; 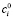 – котировка акции i-го эмитента в момент формирования портфеля;
– котировка акции i-го эмитента в момент формирования портфеля; 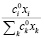 – доля i-го актива в целочисленном портфеле; σij – ковариация i-го и j-го активов в портфеле; ri – средняя ожидаемая доходность i-го актива; F(rnLCn)n – функция модели Марковица от доходности и ликвидности; rn – нормированная доходность i-го актива; LCn – нормированная ликвидность i-го актива; RLCi – ранг ликвидности i-го актива; Ar – весовой коэффициент функции доходности.
– доля i-го актива в целочисленном портфеле; σij – ковариация i-го и j-го активов в портфеле; ri – средняя ожидаемая доходность i-го актива; F(rnLCn)n – функция модели Марковица от доходности и ликвидности; rn – нормированная доходность i-го актива; LCn – нормированная ликвидность i-го актива; RLCi – ранг ликвидности i-го актива; Ar – весовой коэффициент функции доходности.
Приведем модель оптимального инвестиционного портфеля Г. Марковица с группировкой активов по ликвидности. Критерий оптимальности – максимум среднемесячной доходности. Используются весовые коэффициенты ликвидности ценных бумаг.
Приведем модель (2) оптимального инвестиционного портфеля В. Шарпа с группировкой активов по ликвидности. Критерий оптимальности – максимум среднемесячной доходности, деленной на риск с учетом ликвидности, с использованием весовых коэффициентов ликвидности ценных бумаг.
При описании модели (2) будем использовать следующие обозначения переменных и параметров: i, j – акции из пула финансовых инструментов инвестора; xi – количество акций i-го эмитента в портфеле (целое положительное число); M – бюджет инвестора; 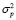 – уровень риска (волатильности) портфеля за период владения ценными бумагами;
– уровень риска (волатильности) портфеля за период владения ценными бумагами; 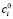 – котировка акции i-го эмитента в момент формирования портфеля;
– котировка акции i-го эмитента в момент формирования портфеля; 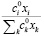 – доля i-го актива в целочисленном портфеле; σij – ковариация i-го и j-го активов в портфеле; ri – средняя ожидаемая доходность i-го актива;
– доля i-го актива в целочисленном портфеле; σij – ковариация i-го и j-го активов в портфеле; ri – средняя ожидаемая доходность i-го актива; 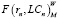 – функция модели Г. Марковица от доходности и ликвидности с использованием весовых коэффициентов ликвидности; WLC – весовой коэффициент группа ликвидности i-го актива.
– функция модели Г. Марковица от доходности и ликвидности с использованием весовых коэффициентов ликвидности; WLC – весовой коэффициент группа ликвидности i-го актива.
Ниже при описании модели (3) будем использовать следующие обозначения переменных и параметров: i, j – акции из пула финансовых инструментов инвестора; xi – количество акций i-го эмитента в портфеле (целое положительное число); M – бюджет инвестора; 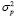 – уровень риска (волатильности) портфеля за период владения ценными бумагами;
– уровень риска (волатильности) портфеля за период владения ценными бумагами; 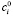 – котировка акции i-го эмитента в момент формирования портфеля;
– котировка акции i-го эмитента в момент формирования портфеля; 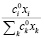 – доля i-го актива в целочисленном портфеле; σij – ковариация i-го и j-го активов в портфеле; ri – средняя ожидаемая доходность i-го актива;
– доля i-го актива в целочисленном портфеле; σij – ковариация i-го и j-го активов в портфеле; ri – средняя ожидаемая доходность i-го актива; 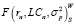 – функция модели В. Шарпа от доходности, риска и ликвидности с использованием весовых коэффициентов ликвидности; WLC – весовой коэффициент группа ликвидности i-го актива.
– функция модели В. Шарпа от доходности, риска и ликвидности с использованием весовых коэффициентов ликвидности; WLC – весовой коэффициент группа ликвидности i-го актива.
Приведем модель оптимального инвестиционного портфеля В. Шарпа с группировкой активов по ликвидности (3).
Построим модель (4) оптимального портфеля Г. Марковица для умеренно-агрессивного инвестора с учетом ликвидности активов с небольшим бюджетом (500 000 руб.). Критерий оптимальности – максимум среднемесячной доходности с учетом ликвидности. Структура и характеристики оптимального портфеля наглядно представлены в таблицах 1 и 2.
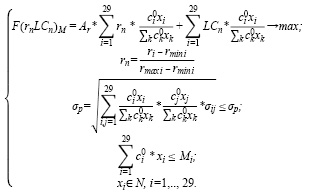 (1)
(1)
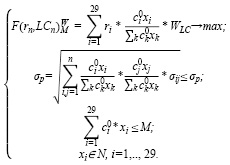 (2)
(2)
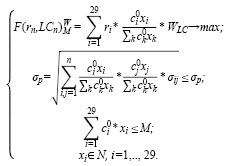 (3)
(3)
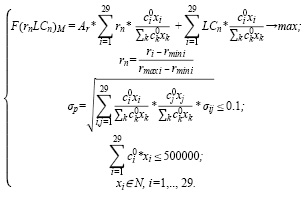 (4)
(4)
Построим модель (5) оптимального портфеля Г. Марковица с группировкой активов по ликвидности для умеренно-агрессивного инвестора с небольшим бюджетом (500 000 руб.). Критерий оптимальности – максимум среднемесячной доходности с учетом ликвидности, с использованием весовых коэффициентов ликвидности ценных бумаг. Структура и характеристики оптимального портфеля представлены в таблицах 3 и 4.
Таблица 1
Структура оптимального портфеля, построенного по модели Г. Марковица, с учетом фактора ликвидности и ограничением на бюджет 500 000 руб.
|
Код |
Имя ценной бумаги |
Количество ценных бумаг в портфеле |
Доля ценных бумаг в портфеле, % |
|
|
326 |
TATNP |
ПАО «Татнефть» имени В.Д. Шашина, ап |
1262 |
100 |
Источник: составлено авторами.
Таблица 2
Характеристики оптимального портфеля, построенного по модели Г. Марковица, с учетом фактора ликвидности и ограничением на бюджет 500 000 руб.
|
Параметр портфеля |
Значение |
|
Инвестиции в портфель, руб. |
527228 |
|
Среднемесячная доходность составленного портфеля, % |
3,87262 |
|
Среднемесячная доходность составленного портфеля, руб. |
19262,2 |
|
Риск портфеля за период владения ценными бумагами, % |
6,26263 |
|
Среднемесячная доходность, деленная на риск за период владения ценными бумагами |
0,48727 |
Источник: составлено авторами.
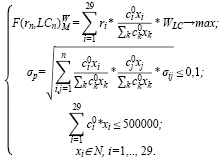 (5)
(5)
Таблица 3
Структура оптимального портфеля, построенного по модели Г. Марковица, с группировкой активов по ликвидности и ограничением на бюджет 500 000 руб.
|
Код |
Имя ценной бумаги |
Количество ценных бумаг в портфеле |
Доля ценных бумаг в портфеле, % |
|
|
323 |
SNGS |
ПАО «Сургутнефтегаз», ао |
19256 |
100,00 |
Источник: составлено авторами.
Таблица 4
Характеристики оптимального портфеля, построенного по модели Г. Марковица, с группировкой активов по ликвидности и ограничением на бюджет 500 000 руб.
|
Параметр портфеля |
Значение |
|
Инвестиции в портфель, руб. |
57189 |
|
Среднемесячная доходность составленного портфеля, % |
2,17634 |
|
Среднемесячная доходность составленного портфеля, руб. |
19233,65 |
|
Риск портфеля за период владения ценными бумагами, % |
6,37723 |
|
Среднемесячная доходность, деленная на риск за период владения ценными бумагами |
0,81735 |
Источник: составлено авторами.
Построим модель (6) оптимального портфеля В. Шарпа с группировкой активов по ликвидности для умеренно-агрессивного инвестора с небольшим бюджетом (500 000 руб.). Критерий оптимальности – максимум среднемесячной доходности, деленной на риск, с учетом ликвидности, с использованием весовых коэффициентов ликвидности ценных бумаг. Структура и характеристики оптимального портфеля представлены в таблицах 5 и 6.
Таким образом, в оптимальный портфель, построенный по модели Г. Марковица с учетом фактора ликвидности, входят 1262 привилегированных акций ПАО «Татнефть» им. В.Д. Шашина. В портфель, построенный по модели Марковица с группировкой активов по ликвидности, входят 19256 обыкновенных акций ПАО «Сургутнефтегаз».
В оптимальный портфель, построенный по модели Шарпа, входят 49261 обыкновенных акций ПАО «Московский кредитный банк», 368 обыкновенных акций ПАО «Газпром» и 24 обыкновенных акций ПАО «Нефтяная компания «ЛУКОЙЛ».
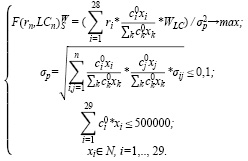 (6)
(6)
Таблица 5
Структура оптимального портфеля, построенного по модели Шарпа, с группировкой активов по ликвидности и ограничением на бюджет 500 000 руб.
|
Код |
Имя ценной бумаги |
Количество ценных бумаг в портфеле |
Доля ценных бумаг в портфеле, % |
|
|
3 |
CBOM |
ПАО “Московский Кредитный Банк”, ао |
49261 |
69% |
|
7 |
GAZP |
ПАО «Газпром», ао |
368 |
20% |
|
10 |
LKOH |
ПАО «Нефтяная компания «ЛУКОЙЛ», ао |
24 |
11% |
Источник: составлено авторами.
Таблица 6
Характеристики оптимального портфеля, построенного по модели Шарпа, с группировкой активов по ликвидности и ограничением на бюджет 500 000 руб.
|
Параметр портфеля |
Значение |
|
Инвестиции в портфель, руб. |
528373 |
|
Среднемесячная доходность составленного портфеля, % |
1,9372 |
|
Среднемесячная доходность составленного портфеля, руб. |
3683,82 |
|
Риск портфеля за период владения ценными бумагами, % |
1,3627 |
|
Среднемесячная доходность, деленная на риск за период владения ценными бумагами |
0,7266 |
Источник: составлено авторами.
Инвестиции в портфель, построенный по модели Марковица с учетом фактора ликвидности, составили 528 373 руб., что на 1,23% больше, чем инвестиции в портфель по модели Г. Марковица с группировкой активов по ликвидности и на 0,05% больше, чем инвестиции в портфель, построенный по модели Шарпа с группировкой активов по ликвидности.
В то же время наибольшая среднемесячная доходность наблюдается для портфеля, построенного по модели Г. Марковица с учетом фактора ликвидности (3,56%), что на 1,15% больше, чем среднемесячная доходность портфеля, построенного по модели Марковица с группировкой активов по ликвидности, и на 1,87% больше, чем среднемесячная доходность портфеля, построенного по модели В. Шарпа с группировкой активов по ликвидности.
Наименьшее значения показателя среднемесячной доходности, деленной на риск за период владения ценными бумагами, наблюдается для портфеля, построенного по модели Г. Марковица с группировкой активов по ликвидности (0,342). Полученные портфели значительно отличаются по структуре.
2. Структура и характеристика оптимальных портфелей, построенных по моделям Г. Марковица и В. Шарпа для инвестора с бюджетом 2 млн руб.
Построим модель (7) оптимального портфеля Марковица для умеренно-агрессивного инвестора с учетом ликвидности активов со средним бюджетом (2 000 000 руб.). Критерий оптимальности – максимум среднемесячной доходности с учетом ликвидности. Структура и характеристики оптимального портфеля представлены в таблицах 7 и 8.
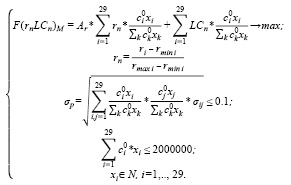 (7)
(7)
Таблица 7
Структура оптимального портфеля, построенного по модели Марковица, с учетом фактора ликвидности и ограничением на бюджет 2 000 000 руб.
|
Код |
Имя ценной бумаги |
Количество ценных бумаг в портфеле |
Доля ценных бумаг в портфеле, % |
|
|
26 |
TATNP |
ПАО «Татнефть» имени В.Д. Шашина, ап |
3943 |
100 |
Источник: составлено авторами.
Таблица 8
Характеристики оптимального портфеля, построенного по модели Марковица, с учетом фактора ликвидности и ограничением на бюджет 2 000 000 руб.
|
Параметр портфеля |
Значение |
|
Инвестиции в портфель, руб. |
2647767 |
|
Среднемесячная доходность составленного портфеля, % |
3,35754 |
|
Среднемесячная доходность составленного портфеля, руб. |
67175,5 |
|
Риск портфеля за период владения ценными бумагами, % |
6,7634 |
|
Среднемесячная доходность, деленная на риск за период владения ценными бумагами |
0,57549 |
Источник: составлено авторами.
Построим модель (8) оптимального портфеля Г. Марковица с группировкой активов по ликвидности для умеренно-агрессивного инвестора со средним бюджетом (2000000 руб.). Критерий оптимальности – максимум среднемесячной доходности с учетом ликвидности и с использованием весовых коэффициентов ликвидности ценных бумаг. Структура и характеристики оптимального портфеля представлены в таблицах 9 и 10.
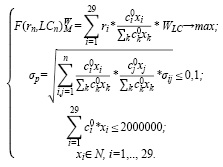 (8)
(8)
Таблица 9
Структура оптимального портфеля, построенного по модели Марковица, с группировкой активов по ликвидности и ограничением на бюджет 2 000 000 руб.
|
Код |
Имя ценной бумаги |
Количество ценных бумаг в портфеле |
Доля ценных бумаг в портфеле, % |
|
|
23 |
SNGS |
ПАО «Сургутнефтегаз», ао |
69635 |
100,00 |
Источник: составлено авторами.
Таблица 10
Характеристики оптимального портфеля, построенного по модели Марковица, с группировкой активов по ликвидности и ограничением на бюджет 2 000 000 руб.
|
Параметр портфеля |
Значение |
|
Инвестиции в портфель, руб. |
2854643 |
|
Среднемесячная доходность составленного портфеля, % |
2,310765 |
|
Среднемесячная доходность составленного портфеля, руб. |
46275,3 |
|
Риск портфеля за период владения ценными бумагами, % |
7,75437 |
|
Среднемесячная доходность, деленная на риск за период владения ценными бумагами |
0,29234 |
Источник: составлено авторами.
Построим модель (9) оптимального портфеля Шарпа с группировкой активов по ликвидности для умеренно-агрессивного инвестора со средним бюджетом (2000000 руб.). Критерий оптимальности – максимум среднемесячной доходности, деленной на риск, с учетом ликвидности и с использованием весовых коэффициентов ликвидности ценных бумаг. Структура и характеристики оптимального портфеля представлены в таблицах 11 и 12.
Таким образом, в оптимальный портфель, построенный по модели Г. Марковица с учетом фактора ликвидности, входят 3943 привилегированных акций ПАО «Татнефть» им. В.Д. Шашина. В портфель, построенный по модели Г. Марковица с группировкой активов по ликвидности, входят 69635 обыкновенных акций ПАО «Сургутнефтегаз». В оптимальный портфель, построенный по модели В. Шарпа, входят 198453 обыкновенных акций ПАО «Московский кредитный банк», 1452 обыкновенных акций ПАО «Газпром», 89 обыкновенных акций ПАО «Нефтяная компания «ЛУКОЙЛ».
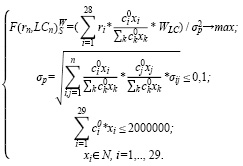 (9)
(9)
Таблица 11
Структура оптимального портфеля, построенного по модели Шарпа, с группировкой активов по ликвидности и ограничением на бюджет 2 000 000 руб.
|
Код |
Имя ценной бумаги |
Количество ценных бумаг в портфеле |
Доля ценных бумаг в портфеле, % |
|
|
3 |
CBOM |
ПАО “Московский Кредитный Банк”, ао |
198453 |
52,7% |
|
7 |
GAZP |
ПАО «Газпром», ао |
1452 |
34,9% |
|
10 |
LKOH |
ПАО «Нефтяная компания «ЛУКОЙЛ», ао |
89 |
12,4% |
Источник: составлено авторами.
Таблица 12
Характеристики оптимального портфеля, построенного по модели Шарпа, с группировкой активов по ликвидности и ограничением на бюджет 2 000 000 руб.
|
Параметр портфеля |
Значение |
|
Инвестиции в портфель, руб. |
224349 |
|
Среднемесячная доходность составленного портфеля, % |
1,57432 |
|
Среднемесячная доходность составленного портфеля, руб. |
31856,5 |
|
Риск портфеля за период владения ценными бумагами, % |
1,69854 |
|
Среднемесячная доходность, деленная на риск за период владения ценными бумагами |
0,94538 |
Источник: составлено авторами.
Инвестиции в портфель, построенный по модели Г. Марковица с учетом фактора ликвидности, составили 224349 руб., что на 0,018% меньше, чем инвестиции в портфель, построенный по модели Г. Марковица с группировкой активов по ликвидности, и на 0,0056% меньше, чем инвестиции в портфель, построенный по модели Шарпа с группировкой активов по ликвидности. В то же время наибольшая среднемесячная доходность – у портфеля, построенного по модели Г. Марковица с учетом фактора ликвидности (3,45%), что на 1,06% больше чем среднемесячная доходность портфеля, построенного по модели Г. Марковица с группировкой активов по ликвидности, и на 1,82% больше, чем среднемесячная доходность портфеля, построенного по модели В. Шарпа с группировкой активов по ликвидности. Наименьшее значения показателя среднемесячной доходности, деленной на риск, за период владения ценными бумагами, наблюдается для портфеля, построенного по модели Г. Марковица с группировкой активов по ликвидности (0,232). Полученные портфели значительно различаются по структуре. Однако, они идентичны портфелям, полученными для бюджета, равного 500000 руб.
3. Структура и характеристика оптимальных портфелей, построенных по моделям Г. Марковица и В. Шарпа для инвестора с бюджетом 10 млн руб.
Построим модель (10) оптимального портфеля Марковица для умеренно-агрессивного инвестора с учетом ликвидности активов с большим бюджетом (10000000 руб.). Критерий оптимальности – максимум среднемесячной доходности с учетом ликвидности. Структура и характеристики оптимального портфеля представлены в таблицах 13 и 14.
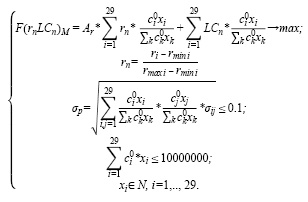 (10)
(10)
Таблица 13
Структура оптимального портфеля, построенного по модели Марковица, с учетом фактора ликвидности и ограничением на бюджет 10 000 000 руб.
|
Код |
Имя ценной бумаги |
Количество ценных бумаг в портфеле |
Доля ценных бумаг в портфеле, % |
|
|
26 |
TATNP |
ПАО «Татнефть» им. В.Д. Шашина, ап |
19764 |
100 |
Источник: составлено авторами.
Таблица 14
Характеристики оптимального портфеля, построенного по модели Марковица, с учетом фактора ликвидности и ограничением на бюджет 10 000 000 руб.
|
Параметр портфеля |
Значение |
|
Инвестиции в портфель, руб. |
10564367 |
|
Среднемесячная доходность составленного портфеля, % |
3,37433 |
|
Среднемесячная доходность составленного портфеля, руб. |
346577 |
|
Риск портфеля за период владения ценными бумагами, % |
6,48759 |
|
Среднемесячная доходность, деленная на риск за период владения ценными бумагами |
0,6349 |
Источник: составлено авторами.
Построим модель (11) оптимального портфеля Г.Марковица с группировкой активов по ликвидности для умеренно-агрессивного инвестора с большим бюджетом (10000000 руб.). Критерий оптимальности – максимум среднемесячной доходности с учетом ликвидности и с использованием весовых коэффициентов ликвидности ценных бумаг. Структура и характеристики оптимального портфеля представлены в таблицах 15 и 16.
Построим модель (12) оптимального портфеля В. Шарпа с группировкой активов по ликвидности для умеренно-агрессивного инвестора с большим бюджетом (10000000 руб.). Критерий оптимальности – максимум среднемесячной доходности, деленной на риск, с учетом ликвидности, с использованием весовых коэффициентов ликвидности ценных бумаг. Структура и характеристики оптимального портфеля представлены в таблицах 17 и 18.
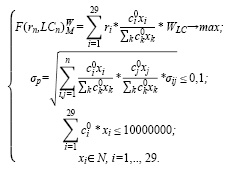 (11)
(11)
Таблица 15
Структура оптимального портфеля, построенного по модели Марковица, с группировкой активов по ликвидности и ограничением на бюджет 10 000 000 руб.
|
Код |
Имя ценной бумаги |
Количество ценных бумаг в портфеле |
Доля ценных бумаг в портфеле, % |
|
|
23 |
SNGS |
ПАО «Сургутнефтегаз», ао |
342863 |
100,00 |
Источник: составлено авторами
Таблица 16
Характеристики оптимального портфеля, построенного по модели Марковица, с группировкой активов по ликвидности и ограничением на бюджет 10 000 000 руб.
|
Параметр портфеля |
Значение |
|
Инвестиции в портфель, руб. |
956841 |
|
Среднемесячная доходность составленного портфеля, % |
2,75438 |
|
Среднемесячная доходность составленного портфеля, руб. |
223795 |
|
Риск портфеля за период владения ценными бумагами, % |
7,89531 |
|
Среднемесячная доходность, деленная на риск за период владения ценными бумагами |
0,28567 |
Источник: составлено авторами.
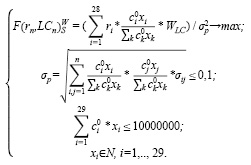 (12)
(12)
Таблица 17
Структура оптимального портфеля, построенного по модели Шарпа, с группировкой активов по ликвидности и ограничением на бюджет 10 000 000 руб.
|
Код |
Имя ценной бумаги |
Количество ценных бумаг в портфеле |
Доля ценных бумаг в портфеле, % |
|
|
3 |
CBOM |
ПАО “Московский Кредитный Банк”, ао |
985632 |
52,7% |
|
7 |
GAZP |
ПАО «Газпром», ао |
59643 |
34,9% |
|
10 |
LKOH |
ПАО «Нефтяная компания «ЛУКОЙЛ», ао |
468 |
12,4% |
Источник: составлено авторами.
Таблица 18
Характеристики оптимального портфеля, построенного по модели Шарпа, с группировкой активов по ликвидности и ограничением на бюджет 10 000 000 руб.
|
Параметр портфеля |
Значение |
|
Инвестиции в портфель, руб. |
1095567 |
|
Среднемесячная доходность составленного портфеля, % |
1,54673 |
|
Среднемесячная доходность составленного портфеля, руб. |
159544 |
|
Риск портфеля за период владения ценными бумагами, % |
1,73469 |
|
Среднемесячная доходность, деленная на риск за период владения ценными бумагами |
0,97321 |
Источник: составлено авторами.
Таким образом, в оптимальный портфель, построенный по модели Г. Марковица с учетом фактора ликвидности, входят 19764 привилегированных акций ПАО «Татнефть» имени В.Д. Шашина. В портфель, построенный по модели Г. Марковица с группировкой активов по ликвидности, входят 342843 обыкновенных акций ПАО «Сургутнефтегаз». В оптимальный портфель, построенный по модели В. Шарпа, входят 985632 обыкновенных акций ПАО «Московский кредитный банк», 59643 обыкновенных акций ПАО «Газпром», 468 обыкновенных акций ПАО «Нефтяная компания «ЛУКОЙЛ».
Инвестиции в портфель, построенный по модели Марковица с учетом фактора ликвидности, составили 1095567 руб., что на 7,34% больше, чем инвестиции в портфель, построенный по модели Г. Марковица с группировкой активов по ликвидности, и на 0,187% больше, чем инвестиции в портфель, построенный по модели. В. Шарпа с группировкой активов по ликвидности. В то же время наибольшая среднемесячная доходность – у портфеля, построенного по модели Г. Марковица с учетом фактора ликвидности (3,45%), что на 1,06% больше, чем среднемесячная доходность портфеля, построенного по модели Г. Марковица с группировкой активов по ликвидности, и на 1,82% больше, чем среднемесячная доходность портфеля, построенного по модели В. Шарпа с группировкой активов по ликвидности. Наименьшее значения показателя среднемесячной доходности, деленной на риск, за период владения ценными бумагами, наблюдается для портфеля, построенного по модели Марковица с группировкой активов по ликвидности (0,232). Полученные портфели значительно различаются по структуре. Следует также отметить, что полученные портфели по структуре идентичны портфелям, полученным для ограничения бюджета, равного 500000 руб., и для ограничения, равного 2000000 руб.
Заключение
Анализ состава и структуры оптимальных портфелей умеренно-агрессивных инвесторов – основной группы профессиональных инвесторов – агентов российского фондового рынка, построенных по моделям Г. Марковица и В. Шарпа, показал их существенное различие для разных уровней инвестиционных бюджетов. При этом структуры оптимальных портфелей, построенных по моделям Г. Марковица и В Шарп с учетом ограничения на ликвидность, сохраняются для различных уровней инвестиционного бюджета. Отмеченное актуализирует проблематику корректного выбора критерия оптимальности с учетом предпочтений инвестора. Включение в модель ограничения на ликвидность портфеля усиливает эти различия. По мнению авторов, использование этого ограничения весьма значимо для модели в постановке Г Марковица. Таким образом, «классический» вариант модели портфеля финансовых активов наиболее точно корреспондируется с алгоритмом поведения инвестора умеренно-агрессивного типа, выбирающего активы для включения в портфель из предварительно составленного списка ликвидных по критериям доходности и риска.
Библиографическая ссылка
Горский М.А., Максимов Д.А. МОДЕЛИРОВАНИЕ ОПТИМАЛЬНОГО ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ УМЕРЕННО-АГРЕССИВНОГО ИНВЕСТОРА С ДОПОЛНИТЕЛЬНЫМ КРИТЕРИЕМ ЛИКВИДНОСТИ // Вестник Алтайской академии экономики и права. 2022. № 2-2. С. 174-189;URL: https://vaael.ru/ru/article/view?id=2074 (дата обращения: 18.02.2026).
DOI: https://doi.org/10.17513/vaael.2074

