Введение
Со времени выхода в свет работ М. Миллера – Ф. Модильяни прошло более полувека, а дискуссия по поводу наличия или, наоборот, отсутствия оптимальной структуры капитала предпринимательской организации, построенной на принципах корпоративного бизнеса, не теряет своей остроты. Напомним, что под оптимальной понимается такая доля собственных (или, напротив, заемных) средств, которая обеспечивает максимальную стоимость свободного денежного потока компании в условиях ограничения на риск события несостоятельности (банкротства).
Если на долгосрочном интервале действует арбитражное правило, обеспечивающее соблюдение условий теоремы М. Миллера – Ф. Модильяни о оптимальности любой структуры капитала корпорации, функционирующей на симметричных и эффективных( без присутствия дополнительных трансакционных издержек обмена активами) рынках, то на кратко- и среднесрочном интервалах основные предпосылки этой теоремы не выполняются, что и актуализирует проблематику выбора оптимальной структуры капитала компании или отдельного ее сегмента (например, производственного (операционного)) в случае одноразовых инвестиций из собственных и привлеченных источников.
Цель статьи – разработка теоретической и методологической базы моделей и методов выбора оптимальной по выбранному и обоснованному критерию структуры рабочего капитала операционного сегмента производственной корпорации с учетом планируемого уровня рентабельности затрат и предельного риска потери финансовой устойчивости основной производственной деятельности.
Материалы и методы исследования
Тематика исследования тесно соприкасается с проблемами моделирования производственной деятельности предприятия корпоративной формы собственности с использованием аппарата производственных функций. Теоретические основы моделирования производственных функций в линейном и нелинейном вариантах, без учета и с учетом риска достаточно подробно рассмотрены в работах А.М. Антиколь и М.А. Халикова [1], М.А. Бендикова и И.Э. Фролова [3], М.А. Горского [5,6,7], В.А. Колемаева [8], Б. Коласса [9], М. Круи [10], М.А. Горского и М.А. Халикова [13], М.А. Халикова, А.И. Дерябиной, Д.А. Лях [14], О.Е. Хрусталева [16], М.А. Горского и Е.М. Решульской [17], Ф. Турино [18] и П. Самуэльсона [19]. Проблематика выбора критериев оптимальности производственной деятельности предприятия а условиях растущих или, наоборот, падающих рынков отражена в работах Д.А. Безухова [2], М.А. Никифоровой и М.А. Халикова [11, 12], М.А. Халикова, Е.С. Кулинченко, А.А. Струковой [15], Математический аппарат, использованный авторами при разработке методов и численных алгоритмов решения задач нелинейной оптимизации заимствован из работ М.А. Горского [4, 6,7], М.А. Горского, М.А. Халикова, Д,А. Максимова [18].
Результаты исследования и их обсуждения
1. Модель выбора оптимального варианта производственной программы предприятия.
Напомним важную для понимания рассматриваемой ниже задачи выбора оптимальной структуры рабочего капитала производственной сферы предприятия модель определения оптимальных номенклатурного и объемного составов производственной программы с учетом фиксированных (заранее определенных) объемов постоянных (F) и переменных (V) активов без детализации источников их финансирования.
Введем следующие обозначения параметров и переменных модели:
i (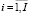 ) – индекс изделия производственной программы;
) – индекс изделия производственной программы;
Si , pi – соответственно, рыночный спрос и цена на i-е изделие;
xi (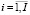 ) планируемый выпуск i-го изделия в выбранном для реализации варианта производственной программы;
) планируемый выпуск i-го изделия в выбранном для реализации варианта производственной программы;
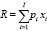 (планируемый валовый доход);
(планируемый валовый доход);
jf ( ), jv (
), jv (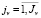 ) – индексы, соответственно, постоянных и переменных активов, учитываемых в калькуляции затрат производственной деятельности предприятия и в составе активов соответствующих групп в рабочем капитале;
) – индексы, соответственно, постоянных и переменных активов, учитываемых в калькуляции затрат производственной деятельности предприятия и в составе активов соответствующих групп в рабочем капитале;
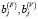 – объемы, соответственно, постоянного (с индексом jF) и переменного (с индексом jV) активов, включенных в планируемые затраты производственного сегмента;
– объемы, соответственно, постоянного (с индексом jF) и переменного (с индексом jV) активов, включенных в планируемые затраты производственного сегмента;
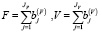 – планируемые на этапе планирования производственной программы совокупные постоянные и переменные активы, учитываемые в оценках, соответственно, постоянных и переменных затрат;
– планируемые на этапе планирования производственной программы совокупные постоянные и переменные активы, учитываемые в оценках, соответственно, постоянных и переменных затрат;
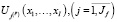 , – функция, (в общем случае нелинейная), отражающая зависимость затрат j-го постоянного актива на реализацию производственной программы, описываемой вектором
, – функция, (в общем случае нелинейная), отражающая зависимость затрат j-го постоянного актива на реализацию производственной программы, описываемой вектором 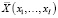 ;
;
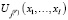 – функция (как правило, линейная – скалярное произведение вектора
– функция (как правило, линейная – скалярное произведение вектора 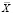 на вектор удельных затрат переменного актива), задающая зависимость затрат j-го переменного актива на реализацию производственной программы, задаваемой вектором
на вектор удельных затрат переменного актива), задающая зависимость затрат j-го переменного актива на реализацию производственной программы, задаваемой вектором 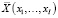 .
.
Простейший вариант модели выбора оптимального по критерию валового дохода варианта производственной программы предприятия задается системой выражений:
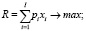 (1)
(1)
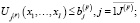 (2)
(2)
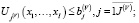 (3)
(3)
x1, …, xI ≥ 0. (4)
Если объемы составляющих постоянных и переменных активов в рабочем капитале не фиксированы и изменяются от одного временного интервала к другому, то можно рассматривать вариант модели, в котором выбираются составы производственной программы и, одновременно, постоянных и переменных активов. В этом случае необходимо учитывать ограничения на доступные объемы финансирования затрат:
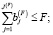 (5)
(5)
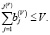 (6)
(6)
В рамках неоклассической теории производства модель (1) – (3), (5), (6), (4) в неявном виде задает зависимость между оптимальной величинами R0 валового дохода, генерируемого в производственной сфере предприятия, и совокупными затратами F и V соответственно постоянных и переменных активов:
R0 = R(F,V) (7)
Таким образом, планируя объемы затрат постоянных и переменных активов, можно рассчитать оптимальный по критерию валового дохода вариант производственной программы предприятия и прогнозируемые показатели эффективности производственной сферы , в частности, рентабельность затрат:
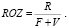 (8)
(8)
Для акционеров и других собственников предприятия важнейшим является показатель отдачи на руб. собственного капитала, вложенного в бизнес или его рентабельность, которая зависит от двух факторов: рентабельности затрат, характеризующей корректность решений, принимаемых в производственной сфере, и структуры пассивов рабочего капитала, характеризующей, с одной стороны, риск несостоятельности корпорации, а, с другой, стоимость привлекаемого в производственную сферу капитала, а следовательно, и уровень затрат в стоимостном выражении. Рассмотрим этот вопрос более подробно.
2. Структура рабочего капитала и рентабельность собственного финансирования производственной сферы предприятия.
Введем следующие дополнительные обозначения для используемых ниже переменных и параметров, характеризующих объемы и стоимость собственных и заемных средств, направляемых на финансирование постоянных и переменных затрат производственной деятельности предприятия (предполагается по умолчанию, что рассматривается конкретный временной интервал t, на котором решается задача оптимизации структуры рабочего капитала):
- def, dev, re – соответственно, доля финансирования постоянных, переменных затрат из собственных источников и цена собственного капитала, размещаемого в пассивах рабочего капитала;
- (1 – def), (1 – devf), rз – соответственно, доля финансирования постоянных, переменных затрат из заемных источников и цена заемного капитала, привлекаемого в пассивы рабочего капитала;
- τ – ставка налога на прибыль предпринимательской организации.
Учитывая альтернативный характер использования собственного и заемного финансирования сферы основного производства предприятия и возможность кумулятивного учета рисков финансирования в ставках доходности различных источников капитала, обоснованным является подход к оценке эффективности выбранной структуры пассивов рабочего капитала, основанный на критерии рентабельности собственного капитала ρСК, рассчитываемом как величина прибыли, генерируемой в производственной сфере, на руб. затрат собственного капитала, направляемого в покрытие полных затрат:
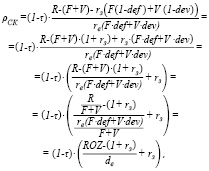 (9)
(9)
где вновь введенные параметры и переменные обозначают:
ROZ – рентабельность полных затрат в варианте производственной деятельности, характеризуемом полными затратами (запланированными) F+V и выпуском продукции (в стоимостном выражении) R (напомним, что выше сделано замечание, что R соответствует максимальному выпуску для полных затрат F+V с учетом производственно-технологических и рыночных ограничений). Таким образом, показатель ROZ рентабельности полных затрат не зависит от структуры пассивов рабочего капитала и является экзогенным параметром для рассматриваемой модели оптимизации структуры рабочего капитала;
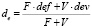 может рассматриваться как показатель средней доли собственного капитала в затратах производственной деятельности предприятия.
может рассматриваться как показатель средней доли собственного капитала в затратах производственной деятельности предприятия.
Преобразим выражение (9) к следующему виду:
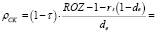
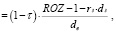 (9’)
(9’)
где dз – аналогично de – средняя доля заемного капитала в полных затратах производственной деятельности предприятия.
Выражение (9’) позволяет привести дополнительные аргументы в пользу обоснованности предложенного показателя эффективности финансирования производственной сферы предприятия:
1. Рентабельность собственного капитала в затратах производственной сферы предприятия снижается с ростом доли собственного (или) цены заемного финансирования;
2. С другой стороны, заемное финансирование производственной сферы оправдано только в случае, если рентабельность затрат по оптимальному варианту производственной программы обеспечивает дополнительные удельные издержки величиной rз · dз по его обслуживанию.
Если рентабельность затрат производственной деятельности предприятия для оптимального варианта его производственной программы обозначить как ROZ0, то средняя доля de собственного капитала в этих затратах на основе выражения (9’) может быть определена как функция от планируемой его рентабельности 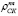 и экзогенных факторов τ и rз по формуле:
и экзогенных факторов τ и rз по формуле:
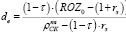 (10)
(10)
или 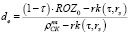 (10’)
(10’)
где rk(τ,rз) – рычаг капитала (или финансовый рычаг) – сумма средств, составляющих экономию предприятия от использования заемного капитала по ставке rз и с учетом налога на прибыль τ.
Связь показателей de и 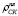 , устанавливаемая выражением (10’), в явном виде отражает их обратную зависимость, отмеченную выше.
, устанавливаемая выражением (10’), в явном виде отражает их обратную зависимость, отмеченную выше.
3. Оптимальная структура рабочего капитала в условиях сокращения объема производства до уровня критического.
На основании выражения (9) из условия равенства валового дохода, генерируемого в производственной сфере предприятия, нулю, получим следующее выражение для критического объема производства:
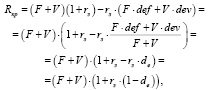 (11)
(11)
позволяющее утверждать о повышении объема безубыточного производства с ростом доли в пассивах рабочего капитала и (или) цены заемного финансирования. В условиях сохранения структуры рабочего капитала и стоимости в нем заемной доли рост критического объема производства обусловлен ростом используемых в производственной сфере постоянных и переменных активов.
Из условия снижения риска наступления события убыточности основной производственной деятельности предприятия, характеризуемого следующим неравенством:
Rкр ≤ (F + V) · (1 + rз · dз), (12)
где dз – 1 – de – средняя доля заемного капитала в затратах производственной деятельности предприятия, получим следующее выражение для минимальной (а, следовательно, и оптимальной с учетом риска структуры рабочего капитала) средней доли заемного капитала:
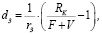 (13)
(13)
где F+V – совокупные затраты, планируемые в производственной сфере для выпуска продукции объемом Rк (в стоимостном выражении).
4. Оптимальная по критерию ρСК структура рабочего капитала в условиях фиксированной и переменной ставок заемного капитала.
Запишем выражение (9) для показателя ρСК отдачи собственного капитала в результатах операционного сегмента предприятия в следующем виде:
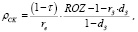 (9’’)
(9’’)
и рассмотрим случай фиксированной ставки rз заемного финансирования затрат производственной сферы предприятия, не зависящей от структуры рабочего капитала. Выпишем условие, при котором ρСК растет с ростом доли dз заемного капитала:
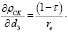
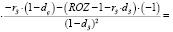
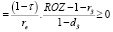 (14)
(14)
Откуда
rз ≤ ROZ – 1. (15)
Таким образом, если цена заемного финансирования операционного сегмента предприятия и рентабельность затрат этого сегмента связаны соотношением (15), то с ростом доли заемных средств в пассивах рабочего капитала растет и отдача собственного капитала. Следовательно, оптимальная доля 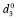 заемного капитала совпадает с предельным уровнем риска структуры рабочего капитала, задаваемого пороговым значением
заемного капитала совпадает с предельным уровнем риска структуры рабочего капитала, задаваемого пороговым значением 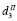 коэффициента финансовой зависимости (
коэффициента финансовой зависимости (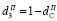 , где
, где 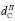 – пороговое значение коэффициента автономии рабочего капитала):
– пороговое значение коэффициента автономии рабочего капитала):
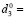
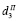 (16)
(16)
Соотношение (16) вполне очевидно: норма доходности капитала, авансированного в покрытие затрат производственной деятельности предприятия, должна быть выше стоимости привлекаемого для заемного капитала, что обеспечивает рост операционного сегмента в условиях растущего рынка готовой продукции.
Второй вывод, вытекающий из неравенства (14), не столь очевиден. Он заключается в том, что с ростом цены re собственного финансирования затрат операционного сегмента предприятия падает отдача заемного финансирования:
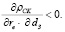 (17)
(17)
Объяснение этому факту следующее. Цена re собственного капитала растет в случае повышения риска операций в сфере производства: за растущий риск собственники требуют адекватную отдачу в форме более высокой доходности акционерного капитала. Растущая стоимость собственного капитала отражается на средневзвешенной стоимости рабочего капитала: ее рост становится причиной роста затрат операционного сегмента, что, в свою очередь, стимулирует снижение отдачи не только полного рабочего капитала, но и отдельных его составляющих, в частности, заемного.
Рассмотрим случай, когда зависимость между ценой и долей заемного капитала в пассивы рабочего капитала операционного сегмента предприятия описывается растущей непрерывной функцией:
rз = rз(dз), (18)
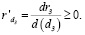 (19)
(19)
Тогда,
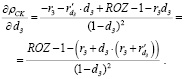 (20)
(20)
Откуда получим аналог неравенства (15) (условие роста отдачи на собственный капитал при увеличении доли заемного) в виде неравенства:
rз + dз · (rз + r’dз) ≤ ROZ – 1 (21)
Учитывая, что в силу (19) выражение rз + dз · (rз + r’dз) – растущая функция переменной dз, можно утверждать, что оптимальная доля 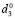 заемного капитала в пассиве рабочего капитала операционной сферы предприятия в случае переменной ставки заемного финансирования, задаваемой функцией (18), может быть получена из соотношения:
заемного капитала в пассиве рабочего капитала операционной сферы предприятия в случае переменной ставки заемного финансирования, задаваемой функцией (18), может быть получена из соотношения:

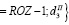 (22)
(22)
Выводы
Обобщая совокупность изложенных в статье результатов, можно сделать основополагающий вывод о актуальности проведенных и будущих исследований в области моделирования оптимальной структуры капитала производственной корпорации, как важного фактора снижения затрат, повышения ее эффективности и конкурентоспособности. В работе получены новые результаты о наличии точки оптимальности в структуре рабочего капитала корпорации для некоторых важных сценариев ее функционирования в турбулентной рыночной среде. Продолжение теоретических изысканий автор видит в практической апробации полученных результатов на информационной базе конкретного предприятия, использующего при финансировании затрат производственной сферы заемный капитал.
Библиографическая ссылка
Аббясова Д.Р. ТЕОРЕТИКО-МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ МОДЕЛИРОВАНИЯ ОПТИМАЛЬНОЙ СТРУКТУРЫ РАБОЧЕГО КАПИТАЛА ПРОИЗВОДСТВЕННОЙ КОРПОРАЦИИ // Вестник Алтайской академии экономики и права. 2022. № 2-2. С. 135-141;URL: https://vaael.ru/ru/article/view?id=2068 (дата обращения: 18.02.2026).
DOI: https://doi.org/10.17513/vaael.2068

