Введение
Сетевая наука со сложными сетями в качестве основной парадигмы привлекает научные общества с их разнообразными практическими возможностями. Научное сообщество успешно описывает синтетические и реальные данные с точки зрения сетевых структур и разрабатывает мощные приложения для дальнейшего эффективного анализа с поддержкой теории графов, теории вероятностей и линейной алгебры.
Чем больше участников в систему, тем больше аргументов в пользу использования сетевого подхода для изучения системы.
Некоторые системы с присущей им веб-природой были интерпретированы как сети, например, транспорт, связь и другие, критически важные инфраструктуры. Туризм [1], поездки на работу [2], торговля [3] – деятельность, связанная с путешествиями, также представлена сетями без проблем. Подобные социальные контакты [4, 5] и соответствующие процессы распространения информации и инфекций [6] имеют одинаковый профиль. Такие системы и данные называются сетевыми объектами [7]. Исследование сетевых объектов [8] представляет особый интерес для различных областей, как теоретических, так и практических [9, 10]. Это традиционный способ изобразить их в формализме теории графов и перемешать слова последней и сетевой науки.
В то же время имеет смысл провести границу между математикой и сетевыми науками, просто чтобы прояснить, на какой области сосредоточены проблемы. Таким образом, если использовать термины «связность», «узлы» и «связи», нет сомнений в том, что в теории графов представлена сетевая наука, а не математика.
Сложные сети расширяют под платформу теории графов, встраивая меры, методы и инструменты, основанные на важных свойствах реальной системы. Инструмент для преобразования так называемых сетевых данных был предложен в работе Дирнбергера М., Келя Т. и Ноймана A. [8].
Однако следует тщательно продумать даже данные сетевого типа, такие как встроенные транспортные системы. Специалистам необходимо принимать во внимание тот факт, что не все сложные сетевые концепции применимы к контексту транспортировки и что некоторая адаптация может потребоваться [11].
Таким образом, для транспортных систем обычно рассматриваются неоднозначные модели, по крайней мере, модели L- и P- [12], как показано в [13] для российских железных дорог (рис. 1).
Что касается пространственных и временных сетей – в отличие от данных (NUD), их сетевые интерпретации весьма разнообразны, и исследователи сталкиваются с трудной проблемой, какой алгоритм преобразования следует применять для лучшего результата.
Материалы и методы исследования
Если традиционно вопросы функционирования актор-сетей изучались непосредственно в плотных городских условиях, то в Байкальском регионе есть возможность сфокусироваться на тех ареалах, где подобные сети имеют наименьшую плотность. Подобная перспектива позволяет более детально рассмотреть влияние каждого участника сети в отдельности, благодаря их разреженности, изучить значимость и прочность тех или иных сетевых связей, и на основе их анализа рассматривать территориальные закономерности формирования социально-экономических ассоциаций.
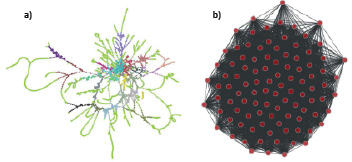
Рис. 1. Российские железные дороги представлены в виде сетевых моделей в L-пространстве (а) и P-пространстве (б) соответственно
Характерно, что АСП описывает любые отношения, которые носят материализованный характер. Участниками отношений могут быть как люди, так и иные сущности, которые, также наделяются субъектностью деятельности, становятся актантами. Полученная в результате анализа актор-сетей информация позволяет далее развивать исследования на платформе комплексных сетей.
Данный подход частично опирается на комплексные исследования, посвященные изучению устойчивого развития туризма [14, 15].
В Байкальском регионе комплексные исследования представлены работами [16, 17]. и др. В работе Даниленко Н.Н. и Рубцова Н.В. [16] рассчитана оценка результативности сферы рекреации и туризма с помощью показателей социально-экономической эффективности на основе официальных статистических данных Иркутскстата и Бурятстата. Однако не решенным остаётся вопрос о соизмеримости различных факторов, влияющих на устойчивое развитие. Кроме того, обобщение туризма как общего набора количественных характеристик оставляет вне пределов внимания разнообразие и роль различных акторов, вовлекаемых в данную сферу.
С другой стороны, используются наработки в сфере изучения лишь единичных факторов (например, только экономические или т.п.). Примерами исследования отдельных факторов являются: оценка рекреационных ресурсов [18, 19]; этнорекреационных ресурсов [17]; транспортной доступности и сезонности [20]; инфраструктуры пространственных данных Байкальского региона [21].
Дополняя проведенные ранее исследования, мы нацелены на детализацию различных акторов, действующих в сфере туризма, и изучение взаимосвязей и взаимозависимости между ними при помощи комбинирования различных методов: наблюдение с элементом описательности; исторический; сравнительный; картографический; аналитико-статистический; экспедиционных исследований; математического моделирования; социологический.
Полученная в результате анализа актор-сетей информация позволит далее развивать исследования на платформе комплексных сетей.
В противоположность акторно-сетевому подходу теория комплексных сетей (ТКС), разграничивает сущности в соответствии с их свойствами. ТКС обратила на себя внимание и зарекомендовала, как надежный подход к решению сложных многоакторных задач в системах любой природы [22, 23]. Важно, что интерпретировать всю сложность систем оказалось возможно широким спектром сетевых представлений, в том числе в виде сетей: временных (динамических) [24], многослойных (мультиплексов) [25], взаимозависимых [26], стволовых [27], комбинированных [28], агрегированных [29], а также их обобщения – кружева единых сетей (КЕС) [30].
В общем, техника отображения временных данных – временных рядов в сложные сети представлена тремя следующими шагами: сегментация по заданной длине времени, огрубление диапазонов, привязка диапазонов с необходимыми весами.
Можно найти множество способов преобразования временных рядов в сложные сети, среди которых можно перечислить:
• Крупнозернистая на основе статистики сегментов (CBS) [31];
• График видимости (VG) [32], а также мультиплексный граф видимости (MVG) [33];
• Локальная сортировка (LS) [34].
В то же время существует несколько надежных практик, которые используют сложные сети для анализа и классификации пространственных данных (изображений или карт).
В работе [35] было продемонстрировано, что при случайном разделении плоскости на пересекающиеся смежные фрагменты можно построить без масштабную сеть, в которой узлы являются фрагментами, а соединения соответствуют общим границам между фрагментами. Это образует «пограничный» подход.
Второй подход можно назвать «пиксельным соседством». Чтобы рассматривать цифровое изображение как сложную сеть: каждый пиксель представляет собой узел; те, которые связаны в соответствии с их окрестности в месте и сходства в интенсивности. Кроме того, был изучен набор сложных сетевых показателей для адекватного моделирования изображений.
Третий подход, так называемый «подход к графам видимости изображений (IVG)» с рядом графов видимости изображений (IVG / IHVG), был представлен как простые алгоритмы, с помощью которых скалярные поля могут отображаться в графы [36].
Представляется целесообразным применить подход только для максимального сохранения внутренней информации исследуемой системы (NUD). Сравнение сетевых подходов может быть качественным и количественным (например, по метрике энтропии).
Модель
В отличие от хорошо известных подходов к отображению NUD (представленных как пространственные и временные данные) в сложные сети с одним масштабом, мы концентрируемся на разделении свойств данных в соответствии с их масштабным разнообразием – по расстоянию, времени и природе. Мы называем этот процесс трансформации очень простым: «сетевая обработка».
Для получения пространственных данных отраженных в карте мы предлагаем трехступенчатый алгоритм сетевизации (на основе методики масштабирования, частично аналогичной предыдущему подходу [37]), который позволяет укрупнить изучаемые области.
Во-первых, внутри выбранной области строится регулярная (или нерегулярная) сеть, размер которой зависит от площади S площади и ее формы (рис. 2).
Количество узлов в зоне Nlocal ~ S.
Два узла соединяются, если расстояние между ними меньше порогового значения (<dcut ). Альтернативным соединением может быть решетчатая сетка. Также имеет смысл построить локальную сеть как регулярную сетку в случае регулярного заполнения узлов.
На втором этапе области в виде огрубленных объектов изображаются узлом или несколькими внутренними узлами (центральными узлами), количество которых зависит от соответствующего размера внутренней сети. Центральные узлы разных областей связаны между собой в случае общей границы между двумя областями (рис. 3). Количество звеньев зависит от длины общей границы: Количество зерен площади (суперузлов) f: Масштаб-> Nгран .
Количество связей между узлами в зернах i и j соответственно с общей границей:
Mзерно i , j ~ L (i, j) / Sum (L (i, j)),
где L – длина границы между i и j зернами.
В-третьих, близкие по природе участки имеют вероятность быть соединенными даже без общей границы и в случае, когда их евклидово расстояние значительно (рис. 4). Вероятность связи между зернами схожей природы P (зерно связи Si,j = 1, если Манхэттенское расстояние (i, j) меньше подходящего порогового значения bотсечения.
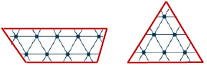
Рис. 2. Шаг № 1 алгоритма, который отображает частицы пространственных данных в сложную сеть: триангуляция

Рис. 3. Шаг № 2 алгоритма, который отображает пространственные данные в сложную сеть: ссылки для огрубленных областей

Рис. 4. Шаг № 3 алгоритма, который отображает пространственные данные в сложную сеть: связь для областей схожего характера
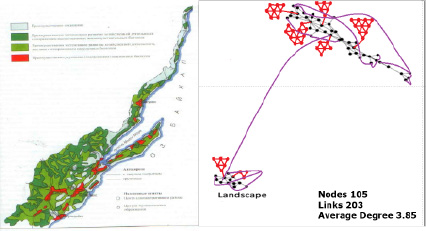
Рис. 5. Сетевое оформление ландшафтной карты Ольхонского района (озеро Байкал)
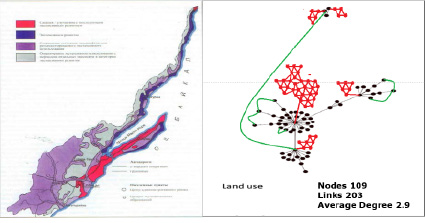
Рис. 6. Сетевизация земельного использования карты, представляющей Ольхонский район (озеро Байкал)
Данная методика масштабирования была применена для создания сети ландшафтных карт и карт землепользования, представляющих Ольхонский район, Иркутская область, РФ вблизи озера Байкал (рис. 5 и рис. 6 соответственно).
Мы обнаружили, что крупнозернистые и зональные соединения полностью формируют без масштабные и свойства малого мира, «резко уменьшая среднюю длину кратчайшего пути» [38] в выходных сетях, тем самым привнося в их структуры реальную сложность.
Генерализация карт привносит некоторые детали и измененные сетевых отпечатков, но не приволит к существенной трансформации топологии сети.
Похоже, что полукачественный и полуколичественный подход к сети, применяемый в работе, и последующий метод, основанный на масштабе, обеспечивают сохранение информации, лежащей в основе NUD, при отображении их в сеть.
Результаты исследования и их бсуждение
В соответствии с Глоссарием IT Gartner и схожими с его терминами оцифровки [39] и цифровизации [40], мы определяем термин «сетевая обработка, или сетирование» как «использование сетевой платформы для изменения научной или бизнес-модели и обеспечения новых достижений и доходов и возможности для создания знаний или создания ценности; это процесс перехода к сетевому домену и обществу в целом». Напротив, «сетевизация» – это «процесс перехода от прямой естественной структурной формы к сети». Другими словами, сетевая обработка берет естественную сущность (систему, процесс и объект) и преобразует ее в сетевую форму без каких-либо других видов изменений самой сущности. Таким образом, можно «объединить в сеть» только сетевые объекты, но для непохожих на сеть объектов, требуется сетевизация.
Приведенные выше примеры сетевизации довольно просты.
Преобразование NUD в многослойные (мультиплексные) сети [41] или в стволовые сети [42] можно рассматривать как многообещающие подходы для тщательного изучения более сложных систем реального мира.
Многозальные сами по себе и стволовой сети компактные модели, которые стратифицируют взаимодействие между субъектами одного и того же типа (как для случаев сетирования и сетевизации). Эти модели были сформированы как известная платформа для исследования сложных систем в различных областях, охватывающих живые организмы, технологические и природные объекты, человеческие общества и другие [43].
Хранение и регистрация больших данных в формате текстов (литература, научные работы, выступления) и пространственно- временной динамики (аудио- и видеозаписи, представленные в медицине, экологии, геологии, метеорологии и других областях) требуют эффективных и действенных инструментов для изучения, и использовать это для национального и международного блага. Создание сети сопряжено с серьезными проблемами при извлечении соответствующей информации из огромных ресурсов данных, передаваемых сетевым (или мультиплексным сетевым) отпечатком для каждого файла. Такой вид дополненной индексации больших данных с использованием сетевых показателей обеспечивает высокую производительность поиска в заданном домене. Это кажется перспективным для обнаружения признаков нежелательных региональных и глобальных процессов, вызванных техногенными и природными факторами.
Выводы
В заключение необходимо отметить, что проведенное исследование показывает, что важно учитывать природу и особенности сети в отличие от данных, рассматривая их как сети. Эта область предоставляет исследователю платформу, которая дает преимущество не терять основную информацию и сохранять ее для анализа и использования в любых областях, в том числе для анализа экономических параметров и управления территориями. Информация, скрытая в NUD, может быть полностью унаследована комплексными сетевыми свойствами, в основном распределением степеней и набором соответствующих показателей, которые выявляются посредством масштабной обработки.
Мы уверены, что подход масштабирования к отображению NUD в сложных сетях может быть ценным и надежным как для пространственных, так и для временных данных. Детализация сетевой модели туристской отрасли с расчетом как отдельных элементов сети, так и агрегированных характеристик сети и её компонентов, сообществ и сети в целом даст возможность выявить структурно уязвимые места в региональной туристической системе, и одновременно предложить топологические решения, выводящие систему на новый уровень развития.
Работа выполнена при частичной финансовой поддержке РФФИ в рамках научного проекта № 18-07-00543 и проекта РФФИ и МОКНСМ в рамках научного проекта № 20-57-44002 «Междисциплинарная сетевая платформа моделирования социально-экономических и экологических процессов на трансграничных территориях РФ и Монголии с ограниченной транспортной доступностью»
Библиографическая ссылка
Труфанов А.И., Куклина М.В., Богданов В.Н., Махакова А.М. ПРЕОБРАЗОВАНИЕ СЕТЕВЫХ ДАННЫХ В СЛОЖНЫЕ СЕТИ: ПРОБЛЕМЫ И ПЕРСПЕКТИВЫ // Вестник Алтайской академии экономики и права. 2022. № 2-1. С. 106-113;URL: https://vaael.ru/ru/article/view?id=2065 (дата обращения: 23.02.2026).
DOI: https://doi.org/10.17513/vaael.2065

