Введение
Начиная с середины 1990-х годов в научной литературе опубликовались работы, посвященные эконофизике. Работы [1-3] посвящены обзору известных в научной литературе попыток провести исследования экономических процессов с использованием теории и методов, разработанных физиками при решении различных физических задач. В работах [4-6] экономические задачи, связанные с колебанием цен и обьема выпуска товаров, с анализом финансовых временных рядов, с объяснением закона спроса и предложения, решаются в рамках физических моделей с использованием математических методов. Автор монографии [7] предлагает теоретико-методологические основы и математический инструментарий эконофизики. В работе определены понятия экономической скорости, экономического ускорения, экономической силы, экономической работы и экономической энергии. Статьи [8-9] посвящены исследованию временной зависимости национального дохода, который удовлетворяет дифференциальному уравнению гармонического осциллятора. В частности, в [9] исследован случай периодической зависимости от времени внешнего воздействия (внешние инвестиции) без учета и с учетом затухания (трансакционные издержки). В настоящей работе решается аналогичная задача, когда внешнее воздействие зависит от времени в виде произведения экспоненты и периодической функции.
Целью исследования является нахождение и анализ национального дохода как функция от времени, удовлетворяющая неоднородному дифференциальному уравнению гармонического осциллятора с внешним возмущением (внешние инвестиции), когда возмущение имеет вид произведения двух функций от времени: экспоненты и периодической функции.
Постановка задачи и её решение
Так как равновесие в макроэкономической системе считается её динамическое состояние в виде колебательного движения с малой амплитудой, то представляет определенный интерес рассматривать динамику изменения национального дохода в модели гармонического осциллятора с возмущением.
Рассмотрим модель осциллятора с внешним возмущением и допустим, что национальный доход как функция от времени (Y(t)) в этой модели без учета затухания (трансакционные издержки) (коэффициент затухания η = 0) удовлетворяет следующему неоднородному обыкновенному дифференциальному уравнению с постоянными коэффициентами второго порядка
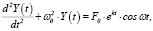 (1)
(1)
где d2Y(t) / dt2 соответствует темпу изменения национального дохода, ω02 · Y(t) ответственен рыночной силе, которая старается возвращать систему к точке равновесия, ω0 – собственная частота колебаний осциллятора, правая часть уравнения показывает внешние инвестиции, меняющихся во времени, k – темп прироста внешних инвестиций, ω – частота колебаний внешних инвестиций, F0 – амплитуда колебаний внешних инвестиций.
Отметим, что если для нахождения общего решения однородного уравнения, соответствующего (1), пользоваться методом Эйлера, а для нахождения одного частного решения неоднородного уравнения (1) пользоваться методом вариации произвольных постоянных, то есть искать в виде
Yч.н.(t) 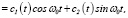 (2)
(2)
то относительно неизвестных c1(t) и c2(t) получим следующую систему уравнений:
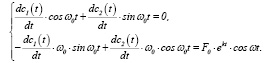 (3)
(3)
Решение (3) приводит к следующим аналитическим выражениям для c1(t) и c2(t)
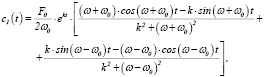 (4)
(4)
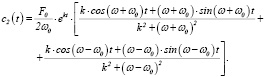 (5)
(5)
Подставляя (4) и (5) в (2) и учитывая, что Yч.н.(t) 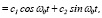 где c1 и c2 – положительные постоянные, после некоторых алгебраических преобразований, получим
где c1 и c2 – положительные постоянные, после некоторых алгебраических преобразований, получим
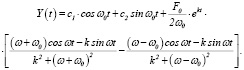 (6)
(6)
Величины c1 и c2 в (6) можно определить из следующих начальных условий Коши
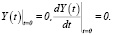 (7)
(7)
Вычисления приводят к выражениям
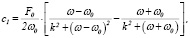 (8)
(8)
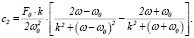 (9)
(9)
В частном случае, когда k = 0 из (6) с учетом (8) и (9) получим
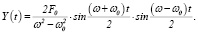 (10)
(10)
Заметим, что последнее совпадает с результатом, полученным в работе [9]. Стоит отметить, что определенный интерес представляет случай резонанса. Выражение для Y(t) в этом случае можно найти, если в (8) перейти к пределу при ω→ω0 с учетом (8) и (9). Итак, имеем
Yрез(t) 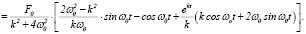 (11)
(11)
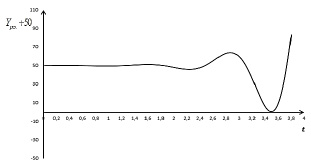
Рис. 1. Кривая изменения Yрез(t) + 50 согласно (11) при η = 0; ω0 = 5; k = 2; F0 = 1; 0 ≤ t ≤ 3,8
Ниже рассмотрим случай, когда η ≠ 0 (учитываем трансакционные издержки). В этом случае в левой части уравнения (1) добавится член 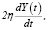 то есть функция Y(t) будет удовлетворять следующему дифференциальному уравнению
то есть функция Y(t) будет удовлетворять следующему дифференциальному уравнению
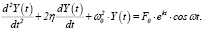 (12)
(12)
Решая однородное уравнение 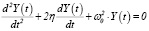 , получим:
, получим:
1. 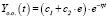 при
при 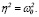 (13)
(13)
2. 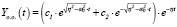 при
при 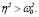 (14)
(14)
3. 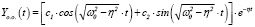 при
при 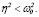 (15)
(15)
Частное решение уравнения (12) будем искать методом подбора, рассматривая следующие случаи: а) k + iω не совпадает с 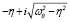 при
при 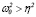
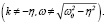
В этом случае Yч.н.(t) ищем в виде
Yч.н.(t) = (Acosωt + Bsinωt) · ekt. (16)
где А и B пока неизвестные коэффициенты. Требуя, чтобы (16) удовлетворяло уравнению (12), для коэффициентов A и B получим
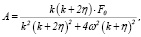
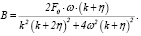 (17)
(17)
Итак, в этом случае общее решение уравнения (12) принимает вид
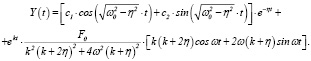 (18)
(18)
б) 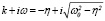
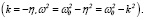
В этом случае Yч.н.(t) будем искать в виде
Yч.н.(t) = t · ekt · (Acosωt + Bsinωt) , (19)
где A и B пока неизвестные коэффициенты. Требуя, чтобы (19) удовлетворяло уравнению (12), для A и B получим
A = 0, B = F0 / 2ω , (20)
Тогда 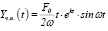 и общее решение уравнения (12) принимает вид
и общее решение уравнения (12) принимает вид
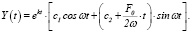 (21)
(21)
Постоянные c1 и c2, которые входят в (18) и (21), находятся с помощью начальных условий Коши (7) и выражаются формулами:
а) 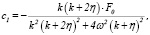 (22)
(22)
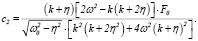 (23)
(23)
б) c1 = c2 = 0. (24)
Ниже приведем общее решение дифференциального уравнения (12) в случаях а) и б).
а) 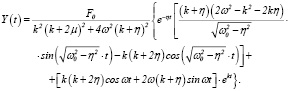 (25)
(25)
б) 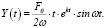 (26)
(26)
Если в (25) и (26) перейти к пределу при ω→ω0 (случай резонанса), то получим выражения для Yрез(t) в случаях а) и б) в виде:
а) 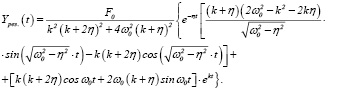 (27)
(27)
б) Yрез(t) 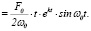 . (28)
. (28)
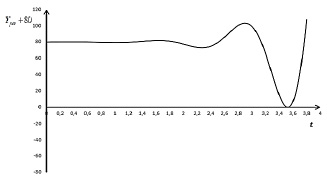
Рис. 2. Кривая изменения Yрез(t) + 80 согласно (27) при 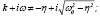 η = 0,1; ω0 = 5,6; F0 = 1; 0 ≤ t ≤ 3,8
η = 0,1; ω0 = 5,6; F0 = 1; 0 ≤ t ≤ 3,8
Из графиков изменения Y(t) в случае резонанса (рис. 1-3) виден колебательный характер динамики национального дохода в зависимости от времени. Во всех трех случаях минимумы и максимумы достигаются почти при одном и том же значении t, но они отличаются своими величинами.
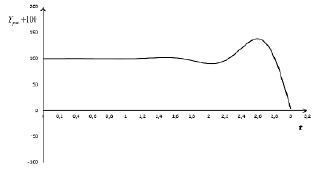
Рис. 3. Кривая изменения Yрез(t) + 100 согласно (28) при 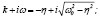 k = 2; η = 0,1; ω0 = 5,6; F0 = 1; 0 ≤ t ≤ 3,8
k = 2; η = 0,1; ω0 = 5,6; F0 = 1; 0 ≤ t ≤ 3,8
Заключение
В работе в физической модели осциллятора с внешним возмущением (внешние инвестиции) исследована динамика изменения во времени национального дохода. Предполагается, что внешние инвестиции зависят от времени в виде произведения показательной функции (экспоненты) и периодической функции. Рассмотрены случаи, когда пренебрегаем трансакционными издержками и когда их учитываем. Проведенный аналитический и графический анализ результатов в случае резонанса показывает, что колебательный характер Y(t) сохраняется. Отметим также, что проведенное в данной работе исследование представляет интерес и с точки зрения развития теоретической эконофизики, и с практической точки зрения возможности использования материалов исследования при чтении курса «Моделирование макроэкономики» для студентов высших учебных заведений.
Библиографическая ссылка
Геворкян Э.А., Сурина Е.Е. ДИНАМИКА ИЗМЕНЕНИЯ НАЦИОНАЛЬНОГО ДОХОДА В МОДЕЛИ ГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА С ВОЗМУЩЕНИЕМ // Вестник Алтайской академии экономики и права. 2022. № 2-1. С. 28-33;URL: https://vaael.ru/ru/article/view?id=2054 (дата обращения: 23.02.2026).
DOI: https://doi.org/10.17513/vaael.2054

