Введение
Эта статья – третья, продолжающая цикл работ д.э.н., профессора кафедры математических методов в экономике РЭУ им. Г.В. Плеханова Халикова Михаила Альфредовича и соискателя по этой кафедре Аббясовой Дианы Рустямовны. Напомним, что в первой публикации по тематике оптимального управления производственной компанией с долгом авторы рассматривали особенности формирования ее дивидендной политики в условиях ограниченного и, напротив, расширенного доступа к внешним источникам финансирования рыночной деятельности. Во второй- особенности выбора и реализации инвестиционных проектов производственной корпорации из собственных и заемных источников финансирования.
Основная идея предыдущих и этой публикаций заключается в разработке инструментария моделей и методов оптимального управления компанией с долгом с учетом ее финансово-экономического положения, доступности и условий получения внешних кредитов, эффективных направлений их использования в сферах производства, финансов и инвестиций.
Цель статьи – разработка теоретической и инструментальной базы выбора оптимальных вариантов производственной деятельности компании и финансирования ее операционного сегмента из собственных и заемных источников с учетом сопутствующих рисков: потери доходности основной деятельности и финансовой устойчивости в сфере производства.
Материалы и методы исследования
Математический аппарат, использованный авторами при разработке методов и численных алгоритмов решения задач нелинейной оптимизации в непрерывном и целочисленном вариантах, частично заимствован из работ Н.С. Бахвалова, Н.П. Жидкова, Г.М. Кобелькова [1], Д.А. Безухова [2], М.А. Бендикова, И.Э. Фролова [3]. При разработке численного алгоритма линеаризации нелинейной дискретной модели авторы использовали идеи метода, предложенного М.А. Горским [4-9].
При изложении тезисов неоклассической концепции производства, эффективности производственных факторов, оценки и управления рисками производственной сферы предприятия авторы активно цитировали работы Г.Б. Клейнера [10,11], Б. Колосса [12], М. Круи [13], А.С. Хасанова [14], О.Е. Хрусталева [15], Р. Дорфмана [16], Д. Луинбергера [17] и др. авторов [18-21],
Результаты исследования и их обсуждения
Опираясь на обоснованный авторами в предыдущих статьях тезис о преимуществах заемного финансирования постоянных и переменных активов рабочего капитала операционного сегмента предприятия, связанных с высокой альтернативной стоимостью собственного капитала корпорации и возможностью в условиях широкого заемного финансирования использования налогового щита, примем, как одно из основных допущений, использование различных (доступных предприятию) источников заемного капитала, объемы которых ограничиваются только потенциалом кредитования банками данного предприятия и предельной величиной риска структуры его рабочего капитала, оцениваемого коэффициентом автономии (долей собственных средства в пассивах рабочего капитала операционного сегмента), рассмотрим математическую модель выбора оптимального авринта производственной программы предприятия и варианта ее финансирования, в которой используем следующие обозначения переменных и параметров:
ƳCK – доля собственного финансирования операционного сегмента предприятия:
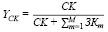 , (1)
, (1)
re – цена собственного капитала, авансированного в покрытие затрат операционного сегмента;
ƳЗKm – доля финансирования операционного сегмента предприятия из m-го внешнего источника (m = 1,M) привлекаемого в покрытие затрат операционного сегмента.
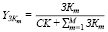 , (2)
, (2)
rm – цена заемного капитала из m-го источника, привлекаемого в покрытие затрат операционного сегмента.
Для переменных и параметров группы «Источники финансирования операционного сегмента предприятия» справедливы следующие балансовые уравнения, структурные ограничения:
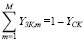 , (3)
, (3)
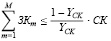 , (4)
, (4)
где ƳCK – фиксированный параметр, в данной модели характеризующий риск структуры рабочего капитала репарационного сегмента;
Если в состав управляемых (эндогенных) параметров модели оптимизации производственной деятельности предприятия и объемов ее финансирования из внешних источников на шаге t включить переменные группы {ЗKm, m = 1,M }, то средневзвешенная стоимость WACCt рабочего капитала и альтернативные затраты RKZAtt на обслуживание капитала операционного сегмента предприятия определяются следующими (соответственно) выражениями:
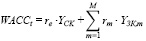 , (5)
, (5)
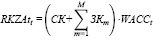 (6)
(6)
(в дальнейшем, рассматривая фиксированный временной интервал t, для упрощения записей формул индекс «t» будем подразумевать).
Для переменных и параметров группы «Изделия производственной программы (ПП), постоянные и переменные активы рабочего капитала операционного сегмента предприятия» будем использовать следующие обозначения и индексы (соответствующие временному интервалу t): i-индекс изделия ПП i (I – число учитываемых в производственной деятельности предприятия изделий); xi – планируемое к производству и реализации на товарном рынке число изделий i-го наименования; xi и xi – соответственно минимальный (исходя из портфеля невыполненных в предыдущем интервале планирования заказов предприятия) и максимальный (отвечающий рыночному спросу) объемы производства и реализации i-го изделия (i = 1,I); pi – прогнозируемая (как правило, средняя за наблюдаемый период t = 1,T) цена реализации единицы i-го изделия в составе выпускаемой партии продукции; Bj – учитываемый по эксплуатационной (или производственной) мощности или в натуральном (стоимостном) выражении запас j-го постоянного или переменного актива, используемого в производстве изделий ПП (J – число учитываемых в калькуляции затрат активов рабочего капитала операционной сферы предприятия; pij – удельные плановые затраты j-го актива (j = 1,J) на производство i-го изделия ПП; dj (j = 1,J) – стоимость восстанавливаемых на последовательных производственно-коммерческих циклах постоянных (в форме затрат на реновацию возобновляемой части) и переменных (в форме пополнения оборотного капитала) активов.
Учитывая широкие альтернативы использования собственного и заемного капитала предприятия не только в операционной, но также и в финансовой, и в инвестиционной сферах деятельности, обоснованным представляется использование в ЭММ выбора оптимальных вариантов ПП предприятия и источников ее финансирования в качестве критерия показателя EVA экономической добавленной стоимости, создаваемой в производственном (jоперационном) сегменте:
EVA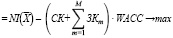 (7)
(7)
где NI(X) – чистая (после налоговая) прибыль на объем производства X, а все приведенные показатели и переменные относятся к временному интервалу t (t = 1,T).
Кроме показателя экономической добавленной стоимости, вполне оправданного для использования в качестве критерия эффективности вложений собственных и заемных средств в операционный сегмент предприятия на кратко- и среднесрочном интервалах планирования (и, в частности, на отдельно рассматриваемом производственно-коммерческом цикле), возможно также использование в качестве такого критерия долевых показателей: прибыль операционного сегмента на руб. собственных или собственных и заемных средств. Так как объем привлекаемых заемных источников ограничен только структурой рабочего капитала, то использование в качестве критерия долевого показателя не приведет к искажению оптимального решения за счет «эффекта структуры».
Основные ограничения статичной модели с критерием (7) включают, кроме структурных (3) и (4) на составляющие пассива рабочего капитала, производственно-технологические, финансово-ресурсные, рыночные и рисковые ограничения, представленные следующими зависимостями:
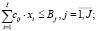 (8)
(8)
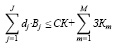 (9)
(9)
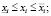 (10)
(10)
CK ≤ PCK; (11)
ƳCK ≥ Ƴ; (12)
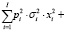
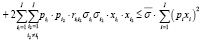 (13)
(13)
где дополнительные обозначения используются для показателей: РСК – полный объем собственных средств в мобильной форме, который может быть привлечен (в периоде t) на финансирование затрат операционного сегмента предприятия; Ƴ – нижний (пороговый) уровень коэффициента автономии рабочего капитала; σi – среднее квадратическое отклонение цены реализации i-го изделия от средней наблюдаемой; 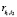 – коэффициент корреляции цен i1-го и i2-го изделий; σ – максимальное значение допустимого рыночного риска изделий ПП.
– коэффициент корреляции цен i1-го и i2-го изделий; σ – максимальное значение допустимого рыночного риска изделий ПП.
Ограничения (8) и (9) можно объединить в одно:
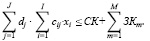 (9’)
(9’)
Авторы специально не конкретизируют аналитическое выражение для чистой (посленалоговой) прибыли, приведенное в соотношении (7), которое корректно определяется с учетом принятой предприятием системы учета доходов и затрат. Для формализации модели достаточно знать, что выпуск 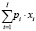 в стоимостном отношении пропорционален затратам переменных и неамортизируемой части постоянных активов.
в стоимостном отношении пропорционален затратам переменных и неамортизируемой части постоянных активов.
Таким образом, ЭММ выбора оптимальных вариантов ПП, источников и объемов финансирования операционного сегмента предприятия включает: критерий в форме (7) или аналогичный, производственно-технологические, финансово-ресурсные, структурные, рыночные, и рисковые ограничения, задаваемые соотношениями (3), (4), (9’), (11), (12), (13), а также дополнительным ограничением на неотрицательность (xi ≥ 0, i = 1,I) или целочисленность (xi Zt, i = 1,I) переменных группы {xi} и неотрицательность переменных группы {ЗКm} (ЗКm ≥ 0, m = 1,M) (ограничение (14)).
Управляемыми параметрами операционного сегмента предприятия при выборе варианта производственной программы и источников и объемов заемного финансирования его производственной деятельности в плановом интервале t являются: РСК – собственный капитал, авансированный в покрытие затрат операционного сегмента; перечень (1,…,М) заемных источников финансирования затрат; ƳCK – доля собственного капитала в общем объеме источников финансирования операционного сегмента, характеризующая риск структуры его рабочего капитала; σ – предельное (пороговое) значение рыночного риска производственной программы, принимаемого собственниками (акционерами) и менеджерами.
Присутствие в модели (7), (3), (4), (9’), (11), (12), (13), (14) ограничения (13) на предельное значение рыночного риска производственной программы позволяет констатировать ее принадлежность к задачам нелинейной дискретной оптимизации (в общем случае, большой размерности), для которых отсутствуют конструктивные (отличные от переборных) численные алгоритмы решения. Для решения задач этого класса (относящихся к NP-полным) можно использовать комбинированные методы и численные алгоритмы, позволяющие получать, как правило, квазиоптимальные (близкие к оптимальным) решения и оценивать величину погрешности.
Рассмотрим один из возможных численных методов поиска квазиоптимального решения нелинейной дискретной задачи (7), (3), (4), (9’), (11), (12), (13), (14).
Сведем эту задачу к задаче линейного непрерывного программирования, сняв ограничения на риск (13) и на целочисленность (14) переменных группы {xi}.
Так как ограничение (13) представлено выпуклым функционалом, то любая линейная комбинация допустимых для исходной (непрерывной) модели решений удовлетворяет и этому ограничению. Учитывая это факт, предлагается найти все базисные решения 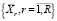 линейной непрерывной задачи (где вектор,
линейной непрерывной задачи (где вектор, 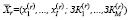 с непрерывными компонентами удовлетворяет всем ограничениям рассматриваемой модели (включая и ограничение (13)), за исключением (14)) и составить их линейную свертку
с непрерывными компонентами удовлетворяет всем ограничениям рассматриваемой модели (включая и ограничение (13)), за исключением (14)) и составить их линейную свертку 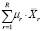 .
.
Решим следующую оптимизационную задачу:
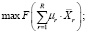 (15)
(15)
μr ≥ 0, r = 1,R; (16)
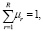 (17)
(17)
где F – критерий исходной линейной непрерывной задачи в форме (7) или выбранной аналогичной.
Пусть μ0r , r = 1,R – оптимальное решение задачи (15) – (17). Тогда квазиоптимальным непрерывным решением линейной непрерывной задачи (7), (3), (4), (5), (9’), (11), (12), (13) будет вектор 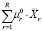 . Точность квазиоптимального непрерывного решения, как это следует из работы М. А. Горского [6], может быть оценена величиной
. Точность квазиоптимального непрерывного решения, как это следует из работы М. А. Горского [6], может быть оценена величиной 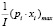 – наибольшее значение компоненты с валовым доходом в расчете на изделие ПП в линейной свертке (15), соответствующей оптимальному решению задачи (15) – (17).
– наибольшее значение компоненты с валовым доходом в расчете на изделие ПП в линейной свертке (15), соответствующей оптимальному решению задачи (15) – (17).
Для нахождения квазиоптимального целочисленного решения исследуемой задачи поступим следующим образом. Поместим квазиоптимальное решение непрерывной задачи в шар радиуса 1 (по каждой компоненте) и расположим все получаемые допустимые (удовлетворяющие ограничениям исходной задачи) решения в лексикографическом порядке (начиная с первой компоненты по возрастанию критерия (7)). Вектор, доставляющий наибольшее значение критерию (7), следует взять за квазиоптимальное решение исходной дискретной нелинейной задачи.
Заключение
В статье рассмотрены постановка задачи и математическая модель выбора оптимальных вариантов производственной программы операционного сегмента предприятия и ее финансирования из собственных и заемных источников с учетом рыночного и финансового риска. Отдельное внимание авторы уделили рассмотрению численного алгоритма решения соответствующей модели нелинейной дискретной оптимизационной задачи большой размерности. В последующих публикациях планируется привести результаты адаптации модели и численного алгоритма на объектах основного производства выбранного производственного предприятия.
Библиографическая ссылка
Аббясова Д.Р., Халиков М.А. ЭКОНОМИКО-МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ОПТИМАЛЬНЫХ ВАРИАНТОВ ПРОГРАММЫ ВЫПУСКА И ФИНАНСИРОВАНИЯ ЗАТРАТ ОПЕРАЦИОННОГО СЕГМЕНТА ПРЕДПРИЯТИЯ С УЧЕТОМ РИСКА // Вестник Алтайской академии экономики и права. 2022. № 2-1. С. 5-10;URL: https://vaael.ru/ru/article/view?id=2050 (дата обращения: 23.02.2026).
DOI: https://doi.org/10.17513/vaael.2050

