Научный журнал

Вестник Алтайской академии экономики и права

Print ISSN 1818-4057

Online ISSN 2226-3977

Перечень ВАК

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Новоселова И.Ю. 1

---

1 Финансовый университет при Правительстве Российской Федерации

В статье рассматривается задача формирования инфраструктурных проектов развития при участии населения и с использованием частичного инвестирования со стороны бизнес-структур. Раскрыта процедура учета мнений групп населения на основе экспертных оценок и их последующей обработки. Для получения экспертных оценок в статье предложена лингвистическая шкала с возможностью перевода в нечеткие треугольные числа, находящиеся в интервале от 0 до 1. Полученные после специальной обработки экспертных оценок приоритеты проектов используются при построении модели формирования набора инфраструктурных проектов, которые будут обеспечены финансированием из бюджета и бизнес-структур. Модель, раскрытая в статье, приведена в двух вариантах: первый вариант ориентирован на финансирование проектов из регионального бюджета, второй – на со-финансирование из регионального бюджета и бизнес-структур. При этом допускается варьирование объемов инвестиций и проведение многовариантных расчетов, которые позволяют получить различные наборы проектов и, соответственно, разный уровень удовлетворения предпочтений населения. Предложенная модель дает возможность провести углубленный анализ вариантов выбора проектов и обеспечить максимальное удовлетворение предпочтений населения. Приведенный численный пример позволяет обеспечить прозрачность предложенной модели.

Статья в формате PDF

439 KB

проекты развития

участие жителей

экспертные оценки

инвестирование проектов

спонсорское участие

оптимальный выбор

нечеткие оценки

1. Яшалова Н.Н., Тюлю Г.М., Чередниченко О.А. Развитие коммунальной инфраструктуры в сельских поселениях в условиях экологизации экономики // Островские чтения. 2019. № 1. С. 197–200.

2. Novoselov A., Potravny I., Novoselova I., Gassiy V. Compensation fund as a tool for sustainable development of the arctic indigenous communities. Polar Science. 2021. Т. 28. С. 100609.

3. Novoselov A., Potravny I., Novoselova I., GassiyV. Sustainable development of the arctic indigenous communities: The approach to projects optimization of mining company. Sustainability (Switzerland). 2020. № 12 (19). Р. 1–18. DOI: 10.3390/su12197963.

4. Юрьева Т. В. Развитие туристской инфраструктуры на основе проектов государственно-частного партнерства // Экономика и предпринимательство. 2021. № 1 (126). С. 622–627.

5. Новоселов А.Л., Новоселова И.Ю. Управление проектами развития территорий // Проблемы региональной экологии. 2020. № 5. С. 134–138.

6. Потравный И.М. Города и поселки российской Арктики: подходы к устойчивому развитию // Экология. Экономика. Информатика. Серия: Системный анализ и моделирование экономических и экологических систем. 2021. Т. 1. № 6. С. 237–242.

7. Мудрецов А.Ф., Тулупов А.С., Прудникова А. А. Социально-экономическое развитие России // Региональные проблемы преобразования экономики. 2017. № 8 (82). С. 4–11.

8. Ухоботов В.И., Стабулит И.С., Кудрявцев К.Н. Сравнение нечетких чисел треугольного вида // Вестник Удмуртского университета. 2019. № 29 (2). С. 197–210. DOI: 10.20537/vm190205.

Введение

Инфраструктура селитебных территорий России непрерывно совершенствуется – восстанавливается исторический облик городов; реставрируются здания; проводится обновление и развитие водоснабжения и водоотведения, транспортных магистралей, систем электроснабжения и отопления; строятся спортивно-оздоровительные комплексы и дома творчества для детей и юношества [1]. В крупных городах развиваются линии метро. Многие малые города России уже сейчас радуют жителей и привлекают туристов уникальными памятниками, уютными улицами, скверами и бульварами. В городах и муниципальных округах России непрерывно проводятся работы по благоустройству территорий – ремонту мостовых и тротуаров; обустройству парков, бульваров, скверов; реставрации памятников истории и архитектуры. Это позволяет восстановить исторический облик городов, сформировать благоприятную среду для отдыха жителей, повысить туристический потенциал региона. Наиболее притягательные проекты благоустройства городских территорий создавались на основе совместной работы жителей микрорайонов и архитекторов. Есть примеры создания народных парков и скверов. Например, в Москве реконструируется и заново создается 40-50 таких рекреационных территорий. Одним из примеров такого рода зон отдыха является преобразованный из пустыря многоуровневый сквер на Ивановской горке в самом центре Москвы. Этот живописный сквер расположен на склоне, по которому проложены лестницы, деревья, газоны и скамейки. Рядом с фонтаном находится памятник истории – сохранившаяся часть крепостной стены из белого камня.

Такие инициативные проекты создаются в рамках московской программы «Народный парк», стартовавшей в 2013 году. Администрация побуждает жителей к формулировке предложений по социально-экологическому развитию их районов и формулирует рамочные варианты проектов. В рамках местного самоуправления жители предлагают будущий облик сквера или парка. Далее профессиональными архитекторами разрабатываются проекты, реализующие предложения жителей. После согласования с инициативной группой жителей эти проекты начинают осуществляться на средства бюджета города или за счет пожертвований структур бизнеса [2, 3, 4].

Особенностью такой схемы сформирования проектов является участие населения в их создании и реализации [5]. Благодаря такому подходу социально-экологическое развития селитебных территорий оказывается соответствующим чаяниям жителей и, следовательно, востребованным [6, 7]. Однако, не все предложенные жителями проекты можно реализовать одновременно, поскольку объема инвестиций недостаточно. Вопрос выбора проектов остается за администрацией муниципального района или города.

Для формализации решения этой проблемы целесообразно разработать количественную характеристику востребованности проектов и процедуру оптимального выбора для реализации в будущем периоде исходя из возможностей инвестирования.

Материалы и методы решения

Решение поставленной задачи проводится в два этапа: на первом этапе выполняется экспертная оценка приоритетности проектов, выполняемые жителями муниципального округа (инициативной группой или на основе дистанционного опроса); на втором этапе решается оптимизационная задача выбора оптимального набора проектов исходя из полученных на первом этапе приоритетов в рамках объема инвестирования.

Для реализации первого этапа предлагается проводить экспертную оценку инициативной группы граждан на основе разработанной шкалы, причем выбор степени приоритетности проекта эксперты основывают на лексических единицах (табл.1, колона 2).

Таблица 1

Основные варианты по шкале оценок предпочтительности проектов социального развития городской агломерации

В таблице представлены пять лексических единиц, которым присвоены номера k = 1,3,5,7,9. Для каждого из этих вариантов установлены границы нечеткой оценки в виде треугольных чисел [8]. Границы нечетких треугольных чисел задаются тремя значениями – максимальным (max), ожидаемым (expected) (exp) и максимальным (max). Т. е. нечеткое число a задается тремя значениями a = (amin, aexp, amax). Для нечетких треугольных чисел задается степень уверенности для каждого граничного значения: μ(amin) = 0, μ(aexp) = 1, μ(amax) = 0. Треугольные числа удобно представить графически, например число a = (2,4,5) представлено на рис. 1.

Воспользовавшись разработанной шкалой, эксперты выбирают один из приведенных вариантов ответов из табл. 1. Если у эксперта возникает сомнение в выборе между представленными вариантами, то принимается промежуточный вариант, для которого границы нечеткой оценки рассчитываются как средние значения границ соседних вариантов. Например, если у эксперта сомнения в выборе между вариантами 5 и 7, то принимается вариант 6, для которого минимальная оценка равна (0,375 + 0,625) / 2 = 0,500; средняя оценка – (0,500 + 0,750) / 2 = 0,625; максимальная оценка – (0,625 + 0,875) / 2 = 0,750. Полная разработанная шкала с промежуточными нечеткими оценками приведена на рис. 2 (промежуточные оценки даны пунктиром).

Воспользовавшись предложенной шкалой, эксперты j = 1,2,…,n выбирают вариант ответа и, тем самым, формируют количественные оценки приоритетности проектов i = 1,2,…,m на основе нечетких треугольных чисел: 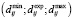. Использование приведенной шкалы позволяет провести оценки согласованности Кендалла на основе номеров вариантов (табл.1, колонка 1). При этом номера вариантов k = 1,2,3,…,9 целесообразно трактовать как ранги.

В случае согласованной оценки, следует определить среднюю нечеткую оценку приоритетности оцениваемых проектов по формуле:

; ;

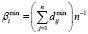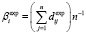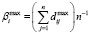(1)

Поскольку для дальнейшего использования, применение нечетких чисел затруднительно, то можно провести дефаззификацию нечетких треугольных оценок приоритетности проектов по формуле:

pi = 0,25(βimin + 2βiexp + βimax) (2)

В результате получены оценки приоритетности проектов pi , i = 1,2,…,m.

На втором этапе решения поставленной задачи требуется осуществление выбора оптимального набора проектов исходя из полученных на первом этапе приоритетов в рамках объема инвестирования. Для этого необходимо сформировать экономико-математическую модель, позволяющую отобрать проекты в рамках выделенных финансовых средств в соответствии с критерием оптимальности позволяющим максимизировать суммарный приоритет проектов. В качестве искомых переменных в модели используются булевские переменные xi, которые принимают значение «единица», если i-ый проект выбирается для реализации, или «ноль» – в противном случае.

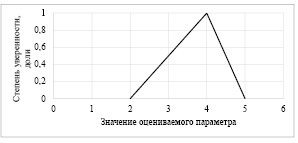
Рис. 1. Пример представления нечеткого треугольного числа

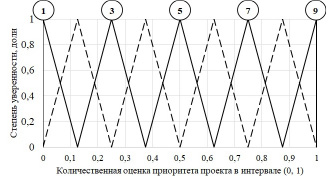
Рис. 2. Графическое представление шкалы нечетких треугольных оценок

Тогда критерий оптимальности модели принимает вид:

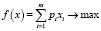(3)

Если проекты финансируются из одного источника (городского бюджета), то ограничение по объему финансирования следует записать в виде:

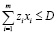(4)

где D – объем финансирования инфраструктурных проектов из городского бюджета;

zi – требуемые для реализации i-ого проекта инвестиции.

Если финансирование осуществляется из нескольких источников, то необходима дополнительная информация о доли затрат λis, которую берет на себя спонсор s (s = 1,2,…,S) при финансировании i-го проекта, а также объем финансирования со стороны каждого спонсора Bs. Очевидно, что доля затрат, которую берет на себя спонсор, находится в пределах: 0 ≤ λis ≤ 1. Если λis = 0, то спонсор не участвует в финансировании i-го проекта; если λis = 1, то спонсор целиком финансирует i-ый проект; если 0 < λis < 1, то спонсор частично финансирует рассматриваемый проект. При этом объем затрат по i-ому проекту, который берет на себя спонсор равен (ziλis). С учетом принятых обозначений получаем систему ограничений по объемам финансирования проектов от всех спонсоров:

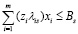, s = 1,2,…,S (5)

С учетом участия всех спонсоров в реализации проектов, оставшуюся часть инвестиций проекты получают из городского бюджета в суммарном объеме не более D. Неудовлетворенная часть финансирования по i-ому проекту равна 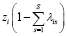. Тогда ограничение по финансированию из городского бюджета примет вид:

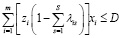(6)

Для отыскания решения поставленной задачи на основе модели (3, 4) или (3, 5, 6) целесообразно воспользоваться одним из методов дискретного программирования с булевыми переменными.

Результаты исследования и их обсуждение

Численное решение задачи

Предложенная модель была использована для решения ряда практических задач. В качестве примера рассмотрим девять проектов, которые были оценены шестью экспертами. Полученные оценки приоритетности по разработанной шкале (табл. 1) приведены в табл. 2.

Результаты расчета оценки согласованности W=0,71 показывают достаточно высокую согласованность мнений экспертов и повторный этап экспертизы не требуется.

Таблица 2

Результаты оценки проектов экспертами

Таблица 3

Результаты обработки экспертной оценки приоритетности проектов

Таблица 4

Затраты на реализацию инфраструктурных проектов

На основе формул (1 – 2) была проведена обработка экспертной информации и получены средние оценки приоритетности и их дефаззификация (табл. 3).

При реализации всех проектов сумма приоритетов равна 4,88. Однако всех проекты реализовать невозможно, поскольку для их реализации требуется финансирование на уровне суммы затрат по всем рассматриваемым проектам. Для каждого из проектов требуемые для их выполнения объемы затрат берутся из ранее разработанных технико-экономических обоснований. Затраты по рассматриваемым проектам приведены в табл.4. Сумма затрат по этим проектам равна 419 млн руб. Объем финансирования из городского бюджета в планируемом году составляет 200 млн руб., поэтому требуется выбор части проектов для реализации в планируемом году в рамках выделенных для их реализации бюджетных средств.

На основе приоритетности проектов (табл. 3) и затрат на их реализацию (табл. 4) формируется численный вид модели (3, 4) для определения оптимального набора инфраструктурных проектов:

f(x) = 0,09х1 + 0,89х2 + 0,48х3 +...+ 0,89х9 → max

25х1 + 65х2 + 35х3 + ... + 61х9 ≤ 200

В результате решения данной задачи в оптимальный план входят следующие проекты: 3, 6, 7, 9. При этом суммарное значение приоритетов оказывается равным f(x*) = 2,83, что составляет 58% от максимальной величины приоритетности, достигаемой при реализации всех инфраструктурных проектов.

Полученное решение было скорректировано с учетом вмешательства спонсора в процесс реализации инфраструктурных проектов. Спонсор готов финансировать четыре проекта: проект 2 – до 60%; проект 4 – полностью; проект 5 – до 50%; проект 6 – до 25%. Суммарный объем финансирования проектов со стороны спонсора – не более 100 млн руб. Финансирование проектов из городского бюджета сокращено до 150 млн руб. С учетом спонсорской поддержки, для выбора инфраструктурных проектов необходимо воспользоваться моделью (3, 5, 6), численный вид которой следующий:

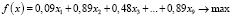
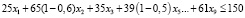
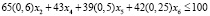
Расчеты позволили определить, что в этом случае будут реализованы проекты 2, 3, 4, 6, 7, т.е. со спонсорским участием три проекта (2, 4, 6). Сумма приоритетов этих проектов оказалась равной 3,18, что соответствует 65,3% от максимальной величины приоритетности. Таким образом, за счет спонсора возросло суммарное удовлетворение приоритета при том, что бюджет направляет 25% (50 млн руб.) на иные городские нужды. Таким образом, приведенный пример показывает расширение возможностей удовлетворения приоритетов населения за счет решения задачи оптимального выбора проектов на основе разработанной экономико-математической модели.

Заключение

Разработанная модель является универсальной – ее можно использовать при формировании любых инфраструктурных проектов для селитебных территорий – городов, сельских поселений и муниципальных районов. Рассматриваемые инфраструктурные проекты могут охватывать широкий спектр аспектов развития – энергетика, транспорт, рекреация, образование, торговля и питание, спорт и проч. Приведенная процедура экспертной оценки приоритетности проектов не требует значительного времени для осмысления экспертами, в качестве которых выступают активные представители населения. Использование нечетких треугольных чисел дает возможность учесть неизбежные ошибки экспертов и получить приоритеты проектов в соответствии с выдвинутыми пожеланиями населения рассматриваемой селитебной территории.

Все экспертные и расчетные процедуры реализованы в системе VBA-Excel, логически и информационно связаны. Это позволяет использовать на практике разработанный подход с любым количеством экспертов и числом проектов. В процессе оптимального выбора проектов в рамках финансирования, могут варьироваться объемы инвестиций, долевое финансирование бизнес-структур. Таким образом, разработанная модель позволяет выполнить многовариантные расчеты, позволяющие представить для обсуждения с населением найденные варианты проектов, чтобы избежать возможных конфликтов из-за отсутствия в плане реализации некоторых из них.

Библиографическая ссылка