Введение
Эта статья – первая, открывающая цикл работ д.э.н., профессора кафедры математических методов в экономике РЭУ им. Г.В. Плеханова Халикова Михаила Альфредовича и соискателя по этой кафедре Аббясовой Дианы Рустямовны по озаглавленной тематике. В первой статье рассматривается постановка соответствующей задачи и возможные теоретические подходы к ее решению. Во второй статье планируется изучить проблематику взаимовлияния долга компании на ее эффективность и стоимость. В последующих работах, которые планируются за подписью Д.Р. Аббясовой, предполагается представить обширный расчетный материал и аналитику по анонсированным исследованиям.
Цель статьи – разработка теоретической базы исследований, увязанных с оценкой и управлением дивидендной политикой корпорации, имеющей свободный доступ на рынок земного капитала для дополнительного рефинансирования деятельности в сферах производства, финансов и инвестиций.
Материалы и методы исследования
Настоящая статья является продолжением исследований проф. М.А. Халикова и его учеников по тематике оценки эффективности и риска не интегрированных и интегрированных в организационную структуру холдинга предприятий. Часть цитируемых источников отражено в ранее опубликованных работах авторов. В рамках этой статьи авторы цитируют многочисленные источники и разработки предшественников – авторов неоклассической производственной функции. В том числе, вид и свойства неоклассической зависимости в паре «выпуск товарной продукции-затраты промизводственных ресурсов» заимствован из работ Г.Б. Клейнера [5,6], Р. Дорфмана, П. Самуэльсона и Р. Солоу [13,17,18]. Необходимо также подчеркнуть определенную связь изложенного материала с работами Д.А. Безухова [2], М.А. Горского [4, 9, 10, 16], Е.М. Решульской [16], Б. Коласса [7], М. Круи [8], Ф. Турино [15], и Ю. Е. Хрусталева [12], посвященными повышению эффективности и устойчивости высокотехнологичных предприятий и холдинг-компаний. Математический аппарат для последующих расчетов по модели оптимального потока дивидендных выплат предполагается организовать на основе авторских разработок с частичным включением работ Н.П. Бахвалова [1] и Д. Лиенберга [13].
Результаты исследования и их обсуждение
1. Постановка задачи оценки и оптимизации стоимости потока дивидендных выплат акционерам предприятия, операционный сегмент которого описывается линейной зависимостью в паре «затраты-выпуск».
Рассмотрим следующую постановку задачи оценки стоимости бесконечного потока дивидендных выплат акционерам и другим собственникам предприятия из нераспределенной прибыли его операционного сегмента в условиях значительного числа допущений, попытка «снятия» части из которых составит предмет исследований одного из следующих разделов статьи.
1-е допущение. Будем считать, что рыночные и внутрифирменные параметры производственного сегмента предприятия (спрос и цены на готовую продукцию, используемые технологии и, главное, зависимость в паре «затраты-выпуск» на бесконечном интервале остаются неизменными, а выпуск продукции описывается линейной функцией от произведенных затрат).
2-е допущение. Затраты производственного сегмента изменяются (в рассматриваемой постановке задачи – растут) пропорционально средневзвешенной стоимости капитала, инвестируемого в производственный сегмент на очередном временном интервале.
3-е допущение. Предполагается, что доля отчислений из нераспределенной прибыли, генерируемой в производственном сегменте предприятия, на непроизводственное потребление и, в частности, на отчисления в дивидендный фонд является величиной постоянной на всем рассматриваемом горизонте.
4-е допущение. Будем предполагать постоянство структуры и составляющих средневзвешенной цены капитала операционного сегмента предприятия на всем рассматриваемом горизонте (как показано ниже, это допущение является наиболее «нереалистичным» из всех приведенных и должно быть «снято» в первую очередь).
С учетом сделанных допущений рассмотрим модель оценки стоимости бесконечного потока дивидендных выплат из прибыли операционного сегмента предприятия, включающую следующие соотношения:
invt = γt · yt , (1)
где invt – инвестиции в рабочий капитал производственного сегмента, сделанные в периоде t из нераспределенной прибыли yt этого сегмента;
γt – доля нераспределенной прибыли, планируемая в инвестиции (в дальнейшем γt = γ ∈ (0; L) – выбранная константа);
divt = (1 – γ) · yt , (2)
где divt – объем отчислений в дивидендный фонд на временном интервале t;
yt+1 = yt · (1 + γ · r*), (3)
где r* – рентабельность рабочего капитала, в общем случае совпадающая с его средневзвешенной ценой:
r* = re · de + rз · (1 – dc), (4)
re – цена собственного капитала, рассчитанная по формуле CAPM с учетом премий на малую капитализацию и отраслевой риск;
rз – цена заемного капитала (эффективная ставка по кредиту за минусом налогового щита);
de – доля собственного капитала в пассивах капитала операционного сегмента.
В силу 4-го допущения r* постоянна на всем рассматриваемом горизонте;
divt+1 = (1 – γ) · yt · (1 + γ · r*), (5)
Если дополнительно предположить, что первые дивиденды выплачиваются по окончании первого из периодов производительного использования рабочего капитала, то, дисконтируя поток дивидендов к началу первого периода по ставке re доходности собственного капитала, размещенного в пассивах операционного сегмента предприятия, получим следующее выражение для стоимости SD бесконечного потока дивидендов:
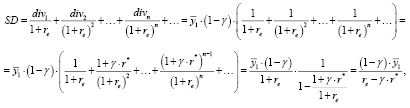(6)
где при выводе соотношения (6) использовалась формула суммы бесконечно убывающей геометрической прогрессии.
Из соотношения (6) непосредственно следует, что при сделанных выше предположениях, справедливы следующие утверждения.
Утверждение 1. При отсутствии внешнего финансирования (для компании без долга), т.е. при r* = re, стоимость полного потока SD дивидендных доходов акционеров и других собственников операционного сегмента предприятия задается формулой (7) бессрочной ренты, а, следовательно, дивидендная политика компании не оказывает существенного влияния на цену акции.
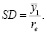(7)
Утверждение 2. Если у компании имеется внешнее финансирование по ставке rз (эффективная ставка по кредиту, уменьшенная на величину налогового щита (1 – τ, τ – ставка налога на прибыль), то:
а) при rз ≥ re предпочтительна консервативная дивидендная политика (не выплачивать дивиденды, приводящая к росту стоимости акций);
б) при rз < re предпочтительна политика полной выплаты дивидендов акционерам (как «премии» за повышенный риск первоначальной инвестиции в рабочий капитал).
Доказательство. Возьмем первую производную от функции SD потока дивидендных выплат по доле γ отчислений на инвестиции в рабочий капитал операционного сегмента:
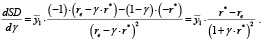(8)
В свою очередь,
r* – re = re · de + rз · (1 – de) – re = re · (de – 1) + rз · (1 – de) = (1 – de) · (rз – re). (9)
Отсюда:
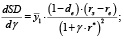(10)
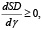если rз ≥ re и 
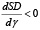, если rз < re ,
т.е. знак монотонности денежного потока дивидендов прямо соответствует знаку выражения rз – re. Утверждение доказано.
2. Постановка задачи оптимизации потока дивидендных выплат из прибыли операционного сегмента предприятия с нелинейной производственной функцией.
Сделаем попытку обобщить полученные в п.1 результаты, частично сняв ограничения, предусмотренные 1-м допущением, а именно, рассмотрим частный случай нелинейной зависимости в паре «затраты-выпуск», описываемой неоклассической производственной функцией степени однородности α (α > 0):
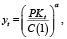(11)
где yt – выпуск продукции (в стоимостном выражении) операционного сегмента предприятия на временном интервале t;
PKt – рабочий капитал (постоянные и переменные активы операционного сегмента на начало временного интервала t, оцениваемые по балансовой стоимости);
C(1) – удельные затраты (себестоимость производства ед. продукции в ед. затрат рабочего капитала).
В свою очередь, рабочий капитал PKt операционного сегмента предприятия на начало временного интервала t – сумма рабочего капитала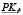 
на конец предыдущего временного интервала t–1 за исключением накопленной за этот период амортизации, собственных инвестиций invt–1 в рабочий капитал по завершении временного интервала t–1 и краткосрочного банковского кредита ЗКt, взятого у кредитной организации по ставке ρ (так как не все из сделанных выше допущений сняты, будем считать, что процентная ставка ρ по кредиту, а также объем кредита и условия кредитования остаются постоянными на всем плановом горизонте).
Таким образом, справедливо соотношение:
PKt = (1 – σ) · PKt–1 + γt–1 · yt–1 + ЗКt , (12)
где σ – норматив амортизационных отчислений. Обозначения остальных параметров и переменных соответствуют приведенным выше.
Если за τ принять налог на прибыль операционного сегмента предприятия, то элемент divt потока дивидендных выплат может быть представлен следующим выражением:
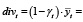
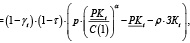(13)
где p – реализационная цена производимой продукции.
Дополнительно введем в рассмотрение коэффициент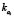 
автономии структуры рабочего капитала для временного интервала t (важный эндогенный (управляемый параметр), манипулируя которым можно повысить/снизить риск структуры капитала и финансовую устойчивость операционного сегмента).
Пусть ka – пороговое значение коэффициента автономии. Тогда, если финансовые рынки не дефицитны, то справедливо соотношение:
ЗКt = PKt · (1 – ka), (14)
С учетом (13) и (14) получим следующее выражение для divt:
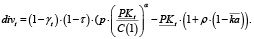(15)
В рассматриваемом случае справедлива ставка r* доходности (средневзвешенная цена) рабочего капитала корректно определяется выражением:
r* = ka · re + (1 – ka) · ρ. (16)
Рассматривая формулы (15) и (16) совместно, делаем вывод, что величина потока дивидендных выплат в условиях низко турбулентных зависит от параметров γt и ka.
Аналогично выражению (6) запишем выражение приведенной к начальному моменту времени стоимости SD бесконечного потока дивидендов из прибыли операционного сегмента предприятия с нелинейной производственной функцией, относящейся к неоклассическим со степенью однородности α (α>0):
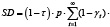
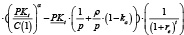(17)
где, напомним, экзогенными параметрами являются: τ – ставка налога на прибыль; p – цена реализации ед. продукции операционного сегмента; C(1) – удельные совокупные затраты на ед. продукции, выпускаемой операционным сегментом; α – степень однородности производственной функции операционного сегмента (α > 0); ρ – ставка по привлекаемым в операционный сегмент внешним кредитам. Эндогенными управляемыми параметрами являются: γt – доля отчислений из нераспределенной прибыли операционного сегмента предприятия в интервале времени t на инвестиции в рабочий капитал; ka – коэффициент автономии в риск структуры пассивов рабочего капитала; re – цена собственного капитала, включенного в рабочий капитал.
Напомним, что в соответствии с выражением (14) коэффициент ka устанавливается на предельном (постоянном) уровне, соответствующим приоритетам финансовой стратегии предприятия. Коэффициент γt и ka изменяются в интервале [0;1].
В выражении (17) используется рекуррентное соотношение (12), связывающие величины рабочего капитала операционного сегмента на последовательных временных интервалах.
Введем в рассмотрение экзогенную константу:
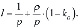(18)
Учитывая, что финансовые и товарные рынки конкурентны, а ставка ρ по кредитку не может превышать рентабельности рабочего капитала и цен рынка готовой продукции, можно утверждать, что l ≈ 1 или l < 1.
Выражение (17) с учетом вновь введенных параметров примет вид:
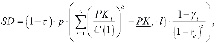(19)
Введем новую константу C = Cα(1) · l и выпишем выражение, описывающее отношение последовательных элементов потока {dt, t ≥ 2}
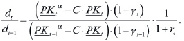(20)
Отсюда получим:
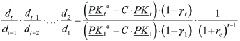
или
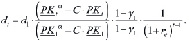(21)
На основании соотношения (21) сформулируем следующее:
Утверждение 3. Если производственная функция операционного сегмента предприятия задается неоклассической зависимостью в паре «затраты-выпуск» степени однородности α > 0, то составляющие дисконтированного к начальному временному интервалу денежного потока дивидендных выплат корректно задаются выражением:
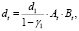(22)
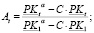
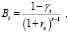
Следствие. Так как знак монотонности dt совпадает со знаками монотонности At и Bt, то стоимость акций компании с долгом для случая нелинейной зависимости в паре «затраты-выпуск» растет пропорционально At и снижается пропорционально Bt.
Учитывая, что At растет с ростом γt , а Bt – снижается, то стратегия заемного финансирования для такой компании неоднозначна: необходим детальный анализ динамики At и Bt, т.е. возникает необходимость экономико-математического моделирования динамики, задаваемого соотношением (22).
Рассмотрим более подробно сомножитель At. Учитывая, что PK1 = PK0 = const (примем за C1), запишем выражение для At в следующем виде:
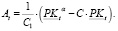(23)
Если учесть соотношения (12) и (14), то для PKt можно записать следующее выражение (выделяя отдельную составляющую, зависящую от выбранного уровня коэффициента ka автономии):
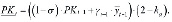(24)
Определим знак производной At по ka:
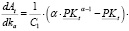
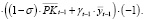(25)
Таким образом, если α < 1 (наиболее распространенный случай), то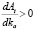 
, а, следовательно, с ростом собственного финансирования затрат операционного сегмента размер дивидендных выплат следует увеличить. Напротив, составляющая Bt (а, следовательно, и dt) монотонно убывает с ростом как доли γt собственных инвестиций в рабочий капитал (что, в принципе, достаточно очевидно), так и цены re собственного капитала в пассивах рабочего капитала.
Итак, в случае нелинейной зависимости в паре «затраты-выпуск» операционного сегмента предприятия его дивидендная политика определяется параметрами ka и re. С ростом коэффициента автономии и (или) снижения стоимости собственного капитала в пассивах рабочего капитала предпочтительна политика роста дивидендных выплат.
В качестве заключительного сформулируем доказанное выше важное
Утверждение 4. Если динамика в паре «затраты-выпуск» в операционном сегменте предприятия описывается неоклассической нелинейной производственной функцией суммарной эластичности α < 1 (наиболее распространенный в экономических приложениях случай), то дивидендная политика предприятия в долгом (ka < 1) консервативна: следует выплачивать дивиденды в полном объеме с ростом доли и (или) стоимости собственного капитала в пассивах операционного сегмента и наоборот, что соответствует также и линейному случаю.
3. Влияние на поток дивидендных выплат компании с долгом изменчивых параметров товарных и финансовых рынков.
Напомним, что в предыдущем разделе, влияние цен товарных и финансовых рынков отражается на коэффициенте l (формулы (18)-(19)), от которого линейным образом зависит поток дивидендных выплат (формула (19)). Если же влияние параметров ρ и p рассматривать в отдельности, то с ростом ρ-ставки заменого финансирования и цены p готовой продукции сокращается валовый доход и, соответственно, поток дивидендных выплат.
Из выражения (18) следует, что этот эффект может быть частично «нивелирован» за счет роста коэффициента ka автономии собственного капитала в пассивах рабочего капитала предприятия и соответственно сокращения долга.
Выводы
Авторами в ходе работы над статьей получены следующие результаты в теории оптимального управления дивидендной политикой компании с долгом. Следующие результаты, в совокупности определяющие научное приращение теории фирмы с долгом:
Доказаны утверждения по постановке задачи оценки и оптимизации стоимости потока дивидендных выплат акционерам предприятия, операционный сегмент которого корректно описывается линейной зависимостью в паре «затраты-выпуск»;
Поставлена задача оптимизации потока дивидендных выплат из прибыли операционного сегмента предприятия с нелинейной производственной функцией;
Сделан вывод о преимуществе политики роста дивидендных выплат с ростом коэффициента автономии и (или) стоимости собственного капитала в пассивах рабочего;
Отражено влияние на поток дивидендных выплат компании с долгих изменчивых параметров товарных и финансовых рынков.
Библиографическая ссылка
Аббясова Д.Р., Халиков М.А. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ОЦЕНКИ ВЛИЯНИЯ СТРАТЕГИИ ВНЕШНИХ ЗАИМСТВОВАНИЙ НА ДИВИДЕНДНУЮ ПОЛИТИКУ КОМПАНИИ // Вестник Алтайской академии экономики и права. – 2021. – № 10-3. – С. 201-207;URL: https://vaael.ru/ru/article/view?id=1907 (дата обращения: 20.04.2024).