Идея создания модели Блэка-Шоулза была впервые опубликована в журнале «Политическая экономия» Ф. Блэком и М. Шоулзом, а затем подробно изложена в «Теории рационального ценообразования опционов» Роберта Мертона в 1973 году.
Использование методов, основанных на инструментарии «реальных опционов», нивелирует недостатки традиционных моделей, при корректном включении параметров, переменных и предположений, на основе которых эти формулы были выведены. Использование теории реальных опционов наиболее важно в случае рассмотрения проектов с неопределенным сценарием окончания, поскольку для их практической оценки не применимы методы дисконтированного денежного потока.
В октябре 1997 г. Нобелевский комитет присудил премию по экономике Р. Мертону и М. Шоулзу. Для присуждения премии комитетом был выдвинут еще один кандидат, Ф. Блэк (Fisher Black), однако он преждевременно умер в 1995 г., что помешало ему разделить с коллегами эту высокую честь. Формула названа именем ее создателей и широко известна в настоящее время – формула Блэка–Шоулза–Мертона (Black–Scholes–Merton option pricing formula) [1]. Эта модель инициировала новую финансовую систему, основанную на торговле опционами, фьючерсами и прочими деривативами и существенно отличающуюся от классического фондового рынка.
Основная идея модели заключается в том, что если базовый актив (актив, включенный в производный финансовый инструмент) торгуется на рынке, то цена опциона на этот базовый актив устанавливается рынком. Ключевым аспектом стоимости является ожидаемая волатильность базового актива: цена может расти или снижаться, что пропорционально отражается на стоимости опциона. Таким образом, текущая стоимость опциона определяет уровень волатильности актива, ожидаемой рынком.
Модель Блэка–Шоулза–Мертона впервые сформулирована в начале 1970–х гг., но ее история начинается гораздо раньше. На рисовой бирже Дойзима в Японии в XVII в. фьючерсные контракты использовали торговцы рисом. В простом фьючерсном контракте дословно утверждалось: «Я согласен купить рис у вас через год по цене, которую мы утвердим прямо сейчас».
К XX в. на американских товарных биржах распространение получили не только фьючерсы, но и опционы (также договорённость о будущей цене, но без обязательства осуществить покупку). Опционы покупались в качестве страховки, на случай неожиданного повышения цены. С течением времени у торговцев ценными бумагами появилась потребность перепродажи опционов, однако с желанием перепродавать опционы у трейдеров возник и вопрос, который поставил торговцев в затруднительное положение, никто не мог ответить «какова же текущая стоимость этих бумаг»?
История модели начинается с работы Луи Башелье в 1900 г., которая была малоизвестна вплоть до 1950-х гг., т. е. до возрождения интереса к ценообразованию опционов [2].
В течение следующих 20 лет было предпринято несколько заметных попыток решить проблему оценки стоимости опциона, и некоторые из ученых действительно приблизились к решению.
Для вывода модели оценки стоимости опциона было необходимо решить несколько важных аспектов, в частности, предположение о том, как изменяется цена базового актива с течением времени. Л. Башелье моделировал движения цен акций в дискретном времени как случайное блуждание. Для генерации случайного блуждания Башелье использовал монету, бросая ее на каждом шаге: если выпадал орел, это означало повышение цены, решка – понижение (рис. 1).
Модель рыночных цен акций Башелье формально предполагала, что цены на акции следуют нормальному распределению. Это хорошо известная кривая колокола, показанная на рисунке 2.
Модель дает реалистичные движения цен на акции в течение короткого периода времени, но не реалистичные – в течение длительного периода, т.к. цена акций, которая изменяется согласно нормальному распределению, может стать отрицательной. В действительности акции могут ничего не стоить, но их цена никогда не может стать отрицательной.
Это является следствием обеспечения ограниченной ответственности. Следовательно, минимально возможное значение цены акции равно нулю.
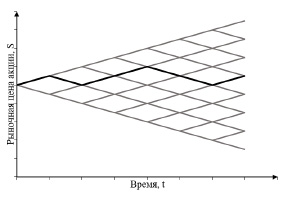
Рис. 1. Пример движения цены акции
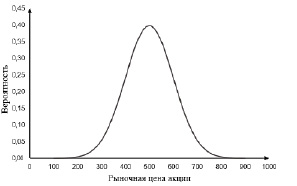
Рис. 2. Нормальное распределение цены акции
Башелье разработал простую формулу оценки опционов, в которой цена актива равна цене исполнения. В терминологии Башелье такие опционы известны как «простые опционы». Башелье заявил, что «цена простого опциона пропорциональна квадратному корню времени». Башелье проверил теоретическую модель, используя фактические опционы, торгуемые на Парижской фондовой бирже. Поскольку у этих опционов были короткие сроки погашения (от одного дня до 45 дней максимум), использование нормального распределения дало разумные результаты. Эта формула по–прежнему действительна в качестве приближения к ценам многих краткосрочных опционов.
Важный научный вклад Л. Башелье в ценообразование опционов не был признан в течение его жизни. Действительно, до недавнего времени мало что известно об отце современной теории ценообразования опционов. Работа Башелье стала широко известна благодаря публикации в 1964 г. книги Павла Кутнера. За публикацией тезисов Башелье последовало 50 – летнее затишье в разработке научной модели для оценки опционов. Однако за это время в мире практических финансов произошли важные изменения. Финансовые рынки стали более важными в экономической жизни, особенно в США, где фондовый рынок пострадал от Великой депрессии и готов был взлететь.
В 1920 г. Бенджамин Грэм запустил то, что мы теперь называем проп– трейдингом – принцип работы финансовой компании, при котором фирма или банк вкладывают средства для достижения своей прямой выгоды, а не зарабатывают комиссионные деньги, торгуя от имени своих клиентов [3]. Грэм считал, что конвертируемые облигации имеют хорошее значение в относительном выражении. Конвертируемая облигация представляет собой пакет, состоящий из долга и опциона колл для покупки обыкновенных акций фирмы. Грэм начал покупать конвертируемые облигации и продавать короткие опционы колл для хеджирования ценового риска. Если такой портфель будет соответствующим образом построен, влияние изменений курса акций на конвертируемую облигацию и короткий опцион колл компенсируют друг друга. Следовательно, эта стратегия может устранить ценовой риск, связанный с движением цен на акции. Грэм также использовал короткие позиции в акции, а также опционы пут для хеджирования риска. Идея объединить разные ценные бумаги в портфеле для хеджирования риска базового актива лежит в основе современного ценообразования опционов.
Опцион колл, встроенный в конвертируемую облигацию, является типом варранта. Варрант по сути является опционом, выпущенным компанией на собственные средства. В некотором смысле они похожи на опционы колл. Основные различия связаны с тем, что варранты выпускаются самой компанией и имеют долгосрочные контракты. В 1920-х гг. варранты стали популярными в США, но в 1930-х гг. они удостоились дурной славы, когда стали ассоциироваться с манипуляциями на фондовом рынке, и избегались до 1965 г., когда компания AT&T выпустила собственные варранты.
Фундаментальный вклад в оценку варрантов внес Пол Самуэльсон. Он предположил, что доходность базового запаса следует логнормальному распределению и получил формулу для цены варранта. Эта формула содержала ряд переменных. Две из этих переменных – ожидаемая доходность акций и ожидаемая доходность варранта. Это были неизвестные переменные, и их было сложно оценить. Если бы Самуэльсон нашел способ получить значения этих двух переменных, он бы решил проблему ценообразования опционов. Ключом к определению значений двух неизвестных была концепция отсутствия арбитража.
Дальнейший вклад в развитие теории ценообразования опционов внесли К. Спренкл, Дж. Бонесс, Ш. Касуф, Э. Торп. Идея Спренкла заключалась в том, чтобы использовать опционы и варранты для того, чтобы вывести ожидания инвесторов относительно прибыли и дисперсии обыкновенных акций. Он разработал формулу ценообразования, которая содержала эти параметры и использовала статистические методы оценки ожиданий рынка. Извлечение ожиданий от цен на производные было довольно проницательным, и этот подход стал мощным инструментом, когда эти рынки стали более развиты.
Бонесс также предположил, что цены на акции распределены логарифмически. Его решение вопроса о ожидаемой ставке доходности заключалось в предположении о необходимости дисконтирования выручки от опциона по ставке ожидаемой нормы прибыли на акцию. Его формула близка к формуле Блэка–Шоулза–Мертона, за исключением того, что она содержит ожидаемую доходность на рынке, в то время как в формуле Блэка– Шоулза–Мертона используется безрисковая ставка доходности.
Э. Торп, также пришел к формуле оценки стоимости опциона, при этом она имела ровно такой же вид, как и формула Блэка–Шоулза–Мертона несколькими годами позже.
Заключительные шаги в решении задачи оценки стоимости опциона были сделаны в работах Ф. Блэка, М. Шоулза и Р. Мертона. В 1965 г. Блэку удалось использовать модель CAPM для получения уравнения цены опциона. Уравнение включало связь между ценой опциона и темпом его изменения в отношении времени, а также цены актива. Такие уравнения известны как дифференциальные уравнения и долгое время использовались в физике и математике, но не в финансах. Окончательное уравнение Блэка для цены опциона не содержало некоторых переменных, которые были включены в него первоначально. Это означало, что конечная формула не будет зависеть от этих переменных. Единственной рисковой составляющей будет являться совокупный риск на акцию, измеряемый его волатильностью. Блэк пытался решить получившееся уравнение, однако вынужден был признать, что это невозможность сделать стандартными методами.
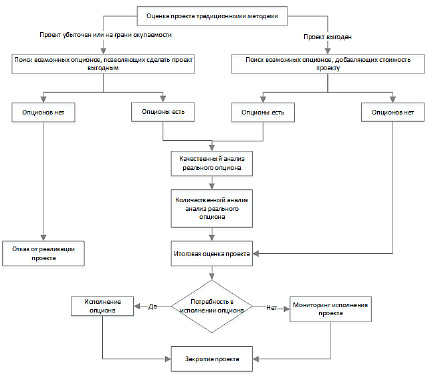
Рис. 3. Алгоритм анализа инвестиционного проекта с применением опционного подхода
Рассмотрим алгоритм применения модели Блэка–Шоулза к оценке реального опциона (рис. 3). В общем случае алгоритм включает следующие этапы:
1. Оценка стоимости инвестиционного проекта традиционными методами анализа;
2. Поиск встроенных в проект реальных опционов. В проекте он может осуществляться как в случае изначальной выгодности, так и если он находится на грани окупаемости или изначально убыточный. Особенную ценность опционный подход представляет тогда, когда более точная оценка стоимости дополнительных выгод от реализации проекта не позволяет отклонить перспективный проект;
3. Определение вида реального опциона, включенного в оцениваемый инвестиционный проект;
4. Определение сути параметров модели Блэка–Шоулза для оценки стоимости реального опциона;
5. Оценка стоимости реального опциона по формуле Блэка–Шоулза;
6. Корректировка изначальной оценки стоимости проекта на стоимость реального опциона и трактовка результата.
Опционный подход в оценке стоимости реальных активов имеет решающее значение в следующем:
− определение различных вариантов развития инвестиционных решений или проектов, которые руководство может осуществить с учетом неопределенных условий ведения бизнеса;
− оценка каждой альтернативы стратегического решения с точки зрения финансовой осуществимости;
− выявление приоритетных путей или проектов на основе серии качественных и количественных показателей;
− оптимизация ценности стратегических инвестиционных решений путем оценки различных путей принятия решений при определенных условиях;
− управление существующими или новыми факторами и стратегическими направлениями принятия решений.
Поиск реальных опционов в проекте может осуществляться как в случае, если проект изначально выгоден, так и, если он находится на грани окупаемости или изначально убыточный. Особенную ценность опционный подход представляет тогда, когда более точная оценка стоимости дополнительных выгод от реализации проекта не позволяет отклонить перспективный проект.
Опционы являются привлекательным инструментом для инвестора по следующим причинам. С одной стороны, в случае если за период владения опционом цена на базовый актив значительно возрастает, то потенциально держатель получит высокую прибыль. При этом она не является ограниченной сверху. С другой стороны – убыток держателя опциона заранее определен. Максимальный проигрыш соответствует величине премии, уплаченной за опцион в момент покупки. Особенно привлекательными являются опционы на такую нестабильную валюту как рубль или акции компаний, производящих инновационное оборудование (компьютерное или ПО). Рынок перечисленных инструментов отличается значительными ценовыми колебаниями в краткосрочном периоде.
Опционный подход к оценке инвестиционных проектов дает иное представление о стоимости проектов. Реальные опционы отражают ценность управленческой гибкости и являются обоснованием интуитивных решений менеджеров, которые не вписываются в рамки традиционной модели. При высокой степени неопределенности результата инвестирования анализ реальных опционов имеет наибольшую потенциальную аналитическую ценность. По прошествии времени направление изменения стоимости базового актива проясняется, тем самым неопределенность уменьшается, тем самым снижается и стоимость опциона. Опционный подход побуждает менеджеров именно в момент времени t взвешивать и анализировать все возможные альтернативы для инвестирования.
Следовательно компании, которые владеют инструментами позволяющими оценить эти возможности количественно могут обосновать инвестиции в проекты, что были отвергнуты конкурентами, которые используют исключительно традиционный подход.
Принципиальное отличие модели Ф. Блэка и М. Шоулза от прочих заключается в том, что их метод не требует выделять премию за риски из стоимости актива. Она не исчезает, а включается непосредственно в цену. Именно этот подход характеризует модель Блэка–Шоулза–Мертона как прорыв в области оценки производных финансовых инструментов. Кроме того, модель косвенно учитывает склонность ЛПР к риску за счет того, что принимать риск будет только тот игрок, который готов и способен рисковать значительными суммами. Это обеспечивает выполнение фундаментальных предпосылок для эффективного управления риском.
При использовании опционного подхода к оценке проектов следует понимать, что реальный опцион не должен быть абстрактным, т.е. оторванным от реальности для лиц, принимающих решения. Менеджеры интуитивно ограниченно применяют опционный подход в том случае, когда откладывают завершение инвестиционной программы до тех пор, пока не будут известны результаты пилотного проекта. Реальные опционы по сути присутствуют в любом инвестиционном проекте, где менеджмент имеет возможность скорректировать курс: увеличить, сократить, задержать или отменить инвестицию. Влияние неопределенности заключается в том, что NPV проекта будет недооценен относительно реального опциона.
Анализ цен опциона Блэка–Шоулза–Мертона обычно применяется к условным требованиям, т. е. ценным бумагам, которые имеют доход, зависящий от прибыли других активов. Анализ условных претензий связан с поиском таких отношений и использованием его для определения цены условного требования. Это те же рассуждения, которые применяются в модели Блэка–Шоулза. Мертон (1998) описывает многочисленные приложения формулы Блэка–Шоулза, которые развивались вместе с финансовыми инновациями.
Одним из значительных применений подхода Блэка–Шоулза–Мертона к ценным бумагам, подобным опционам, является ценообразование на страховые контракты, такие как гарантии по кредитам и политики страхования вкладов. По сути, стратегия приобретения как опциона–пут на актив, так и актива может рассматриваться как политика страхования от убытков, которые могут возникнуть в результате снижения цены актива. Аналогично, гарантии по кредитам и полисы страхования депозитов защищают владельца от убытков, которые могут быть понесены в случае невыполнения обязательств. Кредитные гарантии страхуют банки от потери платежей по кредитам, которые они выдают, должны быть приобретены заемщиком по умолчанию.
Страхование вкладов аналогичным образом является гарантией того, что вкладчики получат полную сумму или некоторый процент от нее в случае дефолта банка. Подробнее объясним сходство страхования вкладов и гарантий по кредитам с опционом–пут. Страховая компания (или правительство) формально выдает опцион–пут, который дает держателю право, но не обязательство продать базовый актив: депозит в банке, где держатель является депонентом, который хочет защитить себя от банкротства банка или выданную ссуду, когда уже банк имеет опцион на кредит и исполнит его в случае дефолта заемщика.
Еще одна сфера применения теории ценообразования опционов – это возобновляемые кредитные соглашения (или линия кредитных соглашений, поскольку они представляют собой один из способов предоставления банками кредитов), которые являются контрактами, аналогичными опционам в том смысле, что компания, нуждающаяся в финансировании ее проектов, подписывает соглашение с другой компанией, которая обязана предоставить первой необходимую сумму, если это потребуется. Компания, которая владеет этим опционом–колл, принимает решение в соответствии со стоимостью заимствований, которую налагают другие банки. В данном случае целью компании является заимствование по самой низкой возможной ставке. Такую теоретическую настройку модели Блэка–Шоулза– Мертона использует Хоккинс (1982) для расчета цен на возобновляемые кредитные соглашения.
Институциональные инвесторы широко используют модель Блэка– Шоулза–Мертона при составлении портфеля ценных бумаг, соответствующего их инвестиционным целям. Производные финансовые инструменты часто предоставляют самый дешевый и эффективный способ для портфельного менеджера изменить инвестиционный микс портфеля. Производные инструменты можно использовать для изменения воздействия портфеля на определенный риск. Например, деривативы акций могут использоваться для изменения воздействия на внутренний рынок ценных бумаг, на внешний рынок или на мировой фондовый рынок. Если портфельный менеджер входит в длинную позицию в фьючерсном контракте, это дает такой же тип риска, как и владение базовой ценной бумагой. Возможно, дешевле и эффективнее использовать фьючерсный контракт, чем покупать базовую ценную бумагу. Производные инструменты также могут обеспечивать защиту от падения путем покупки опционов на покупку или заключения короткой позиции в фьючерсном контракте.
Многие продукты, которые продаются розничным инвесторам в настоящее время, содержат встроенные опционы, и потребитель покупает пакет в виде полного контракта. Например, многие договоры страхования жизни и сбережения содержат встроенные производные инструменты. В США примером являются так называемые аннуитеты с индексом акций.
Если страховая компания продает такие контракты, то она продает опционы колл на базовый портфель акций. Компании не хватает опционов колл, и одним из способов, которыми она может покрыть этот риск, является покупка аналогичного опциона у инвестиционного банка. Риск передан банку, и он может либо хеджировать риск, используя динамическую стратегию хеджирования, либо покупать аналогичные опционы колл на рынке или из другого института. На внебиржевом рынке хедж–фонды являются естественными покупателями этих долгосрочных опционов на акции.
В то время как основная заслуга подхода Блэка–Шоулза–Мертона заключается в его простоте в применении, модель Блэка–Шоулза–Мертона была разработана исключительно теоретически, в результате большая часть литературы по теории ценообразования опционов поставила под сомнение ее предположения: их нереалистический характер может помешать модели производить точные предсказания при эмпирическом тестировании. Другим подходом, используемым при тестировании теории, является сравнение прогнозов модели по ценам опциона с наблюдаемыми рыночными ценами. Если прогнозы будут постоянно точными, модель Блэка–Шоулза–Мертона будет лучшей моделью, независимо от ее допущений.
Библиографическая ссылка
Воротникова Д.В., Максимов Д.А. ОПЦИОННЫЙ ПОДХОД ОЦЕНКИ ИНВЕСТИЦИОННЫХ ПРОЕКТОВ: СТАНОВЛЕНИЕ И СУЩНОСТЬ // Вестник Алтайской академии экономики и права. 2021. № 9-2. С. 117-124;URL: https://vaael.ru/ru/article/view?id=1848 (дата обращения: 18.02.2026).
DOI: https://doi.org/10.17513/vaael.1848

