Исследование возможностей экономико-математического моделирования методологии планирования бюджета хозяйствующего объекта, как уже подчеркивалось, в большой степени опирается на приемы, базирующиеся на эвристическом поиске пути улучшения некоторого варианта бюджетирования, основанного на анализе тенденций изменения конечных результатов. Практической же деятельности присуще стремление к полной автоматизации нахождения рационального варианта, что обычно достигается увеличением степени опоры на математические методы оптимизации.
Это может быть обеспечено, если в общей проблеме оптимизации бюджетирования выделить ряд частных подзадач, которые можно свести к задачам, решаемых математическими методами. К основным из них следует отнести:
1) оценку потребного объема бюджета для достижения желаемых конечных результатов;
2) распределение заданного объема денежных средств по проводимым мероприятиям при заданных значениях конечных показателей;
3) оптимизацию (минимизацию) объема бюджета при установленных ограничениях частных и конечных показателей;
4) оптимизацию распределения денежных средств по мероприятиям при установленном общем объеме бюджета с учетом установленных ограничений частных и конечных показателей.
Решению указанных задач с прямым использованием математических методов в настоящем исследовании способствует создание математической линейной модели [2] бюджетирования, формально представляемой выражением
ΔY = DΔS, (1)
где ΔY – вектор приращений конечных показателей;
ΔS – вектор приращений денежных средств на проведение установленных мероприятий;
D – матрица линейной модели.
Первая и вторая из перечисленных задач может быть решена, будучи сведенной к решению системы линейных уравнений, представленной выражением (1). В развернутом виде эта система записывается как [2]:
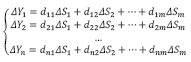 (2)
(2)
где ΔYi (i = 1 ... n) – элементы вектора ΔY размерности n (количество конечных показателей);
ΔSj (i = 1 ... т) – элементы вектора ΔY размерности т (количество мероприятий);
dij (i = 1 ... n, j =1 ... т) – элементы матрицы D размерности п*т;
Решением данной системы является совокупность элементов ΔSj вектора приращений денежных средств на проведение мероприятий при известных величинах приращений ΔYi конечных показателей и элементов dij. Потребный объем бюджета при этом равен сумме
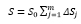 (3)
(3)
где S0 – величина бюджета, потребная для достижения исходных значений конечных показателей.
Потребный объем денежных средств для проведения каждого мероприятия определяется как Sj = Sj0 + ΔSj, где Sj0 – величина денежных средств, определённая в качестве исходной. Методика определения величин Yi0, Sj0, dij, являющихся элементами разработанной линейной модели, представлена в предыдущем параграфе.
Третья и четвертая из перечисленных выше задач могут быть решены путем сведения их к задачам линейного программирования, первая из которых может быть представлена в следующем формализованном виде[8]:
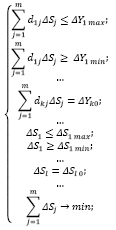 (4)
(4)
где величины ΔYi max , ΔYi min , ΔYk0 , ΔSj max, ΔSj min , ΔSj0 представляют собой ограничения величин конечных показателей, а также денежных средств, определяемые ограничениями частных показателей.
Решение третьей задачи можно представить как комплекс решений подзадач, имеющих следующий вид:
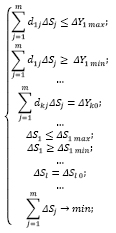 (5)
(5)
Разработка рекомендаций no решению задачи бюджетирования, сводящейся к решению системы линейных уравнений.
Как отмечено выше, к решению системы линейных уравнений сводится задача оценки потребного объема бюджета (по каждому мероприятию и в целом) для достижения желаемых конечных результатов. Эта система представлена выражением (2). В матричной форме она имеет вид DΔS = ΔY0 или
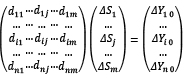 (6)
(6)
где ΔY0 – вектор заданных (желаемых) величин конечных показателей;
ΔS – вектор искомых величин денежных средств, планируемых на проведение мероприятий.
В соответствии с теоретическими выводами линейной алгебры [7] при решении этой системы возможны три случая:
- система не имеет решений (система не совместна);
- система имеет бесконечное множество решений;
- система имеет единственное решение.
Применяя положения линейной алгебры к решению распределения денежных средств, следует учитывать, что в любом из перечисленных случаев, которые могут возникнуть на практике, адаптация этих выводов должна осуществляться так, чтобы ситуация была сведена к нахождению единственного решения. Это означает, что при определённых исходных данных, для которых решение не единственно, необходимо некоторые параметры изменить или дополнить. Это необходимо сделать так, чтобы не потерять сути решаемой экономической задачи. Поэтому следует проанализировать условия появления указанных случаев.
Система линейных уравнений не совместна, если не равны ранги матриц: D и расширенной D1 (rang D ≠ rang D1), где
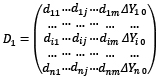 (7)
(7)
Анализ матриц D и D1 показывает, что
- ранг расширенной матрицы D1 всегда не меньше ранга матрицы D (rang D1 ≥ rang D);
- несовместность системы определяется наличием строк, содержащихся в ненулевом миноре, определяющем ранг матрицы D1, и одновременно являющихся линейной комбинацией строк, содержащихся в миноре, определяющем ранг матрицы D.
С учетом этих особенностей структуру матриц D и D1 для общего случая (не обязательно самого распространенного случая, возникающего в практике).
На схеме формул 8 видно, что можно выделить три группы строк матриц:
1) строки, элементы которых используются для расчета некоторого ненулевого минора матрицы D, определяющего ее ранг, т. е. минора, размерность которого равна рангу указанной матрицы;
2) строки, являющиеся линейной комбинацией строк первой группы и одновременно содержащие элементы, используемые для расчета ненулевого минора матрицы D1, определяющего ее ранг. Наличие таких строк также определяет неравенство рангов матриц, что и указывает на несовместность системы;
3) строки, являющиеся линейной комбинацией строк, элементы которых используются для расчета обоих упоминаемых миноров.
Столбцы матрицы D также разделены на две группы (это же деление отображено и на схеме матрицы D1), включающие столбцы, элементы которых используются и не используются для расчета выбранного ненулевого минора матрицы D определяющего ее ранг.
Определитель квадратной матрицы, составленной из группы элементов dij, содержащихся в левой верхней области матрицы D, представляет собой ненулевой минор, определяющий ее ранг.
a) 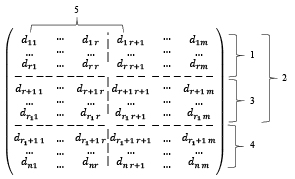 (8)
(8)
б) 
Характеристика элементов матриц D (a) и D1 (б):
1. – базисные строки матрицы В;
2. – строки, входящие в ненулевой минор, определяющий ранг матрицы D1;
3. – строки, являющиеся линейной комбинацией строк, входящих в минор, определяющий ранг только матрицы D;
4. – строки, являющиеся линейной комбинацией строк, одновременно входящих в миноры, определяющие ранг матриц D и D1;
5. – базисные столбцы матрицы D
Строки и столбцы матрицы D, элементы которых используются в расчете выбранного ненулевого минора, определяющего ранг матрицы, будем называть базисным [2].
Строки третьей группы необходимо вообще исключить из процесса решения задачи, т. к. они никак не влияют на результат.
Наличие строк второй группы, как уже отмечалось, указывает на несовместность системы. Разрешить проблему несовместности можно изменением исходных данных, а именно изменением исходных значений конечных показателей ΔY r+10 … ΔY r10, которые соответствуют строкам этой группы. Изменить их следует таким образом, чтобы строки этой группы стали линейной комбинацией базисных строк матрицы D. В этом случае эти строки также можно будет исключить из рассмотрения, т. к. они тоже не будут влиять на результат. Таким образом, при наличии строк второй группы их также следует исключить из решения задачи, но при этом после решения системы из оставшихся уравнений необходимо вычислить измененные значения конечных показателей ΔYr+10 … ΔYr10. Это выполняется с использованием выражений, соответствующих исключенным строкам.
Таким образом, путем исключения строк второй и третьей групп приходим к упрощению матриц, которым и будет соответствовать система линейных уравнений, имеющая решение (9):
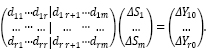
С точки зрения распределения денежного ресурса это означает, что путем анализа исходных данных:
- выявляется наличие тех их них, которые не влияют на результат распределения и, поэтому, должны быть исключены из анализа;
- выявляется наличие тех из них, величины которых противоречат здравому смыслу и должны быть изменены на допустимые значения.
Следующий шаг анализа заключается в выявлении ситуации, связанной с бесконечным множеством решений. Система будет иметь бесконечное множество решений при наличии в матрице D столбцов, не являющихся базисными. Это имеет место в случае, когда число столбцов превышает число строк (число неизвестных превышает число уравнений). В этом случае для получения единственного решения необходимо неизвестным (ΔSj), в количестве т – r, задать некоторые значения. В качестве таковых, должны быть выбраны те (ΔSr+1, … ΔSm), которые не соответствуют базисным столбцам матрицы D. Это означает, что для проведения некоторых планируемых мероприятий нужно предварительно задать величины денежных затрат. Естественно, что в качестве таких мероприятий целесообразно взять те, которые вносят наименьший вклад в достижение конечных результатов, а сами затраты привести к минимальным величинам, оправляемыми ограничениями.
Если все изложенное выполнить, то получим систему, имеющую единственное решение:
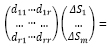
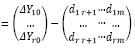 (10)
(10)
С учетом изложенного рекомендации по совершенствованию механизма; распределения денежных средств по проводимым мероприятиям будут выглядеть следующим образом.
1. Должны быть выполнены процедуры до получения матрицы D приращений конечных показателей на единицу денежных средств, вкладываемых в проведение каждого мероприятия, и построен исходный вариант графика нарастания величин конечных показателей по технологии, основанной на подходе «затраты – эффект».
2. Должно быть произведено ранжирование конечных показателей и мероприятий, при котором следует учесть, что:
- ранжирование конечных показателей является весьма условным, – если система (1.5) совместна, то его вообще выполнять нет необходимости. Однако с первого взгляда, особенно при большой размерности матрицы D, оценку совместности системы произвести бывает трудно. Ранжирование выполняется по важности показателя, которая, в свою очередь, определяется тем, какой из показателей будет вычисляться в процессе решения системы уравнений, а какой будет определяться по принципу «какой получится» в случае, если эта система окажется несовместной. Последние считаются менее важными;
- ранжирование мероприятий осуществляется с использованием варианта «затраты – эффект» [3].
3. Матрица D перестраивается по важности строк и столбцов, где строки оцениваются по соответствующим им конечным показателям, а столбцы – по соответствующим мероприятиям.
4. Определяются базисные строки перестроенной матрицы D, для чего последовательно строки, начиная со второй, проверяются на то, является ли она линейной комбинацией предыдущих. Если проверяемая строка является линейной комбинацией, то она исключается из матрицы.
5. Определяются базисные столбцы получившейся матрицы D, для чего последовательно столбцы, начиная со второго, проверяются на то, является ли он линейной комбинацией предыдущих. Если проверяемый столбец является линейной комбинацией, то ему изменяют место в иерархии, и он выводится из зоны группы базисных столбцов. В результате получается матрица D, отображенная в системе (10).
6. Для проведения мероприятий, соответствующих столбцам, не вошедшим в группу базисных, устанавливаются конкретные денежные затраты (ΔSr+1 ,… ΔSm). Как уже отмечалось, эти затраты целесообразно определить на основе существующих ограничений на величины частных показателей. В результате получается система линейных уравнений (11), имеющая единственное решение.
7. Осуществляется решение системы (11). В результате решения получают величины денежных затрат ΔS1 , … ΔSr , которые совместно с установленными в п. 10, представляют оценку потребного объема бюджета для достижения желаемых конечных результатов. Далее следует оценить полученный результат на предмет нарушений установленных ограничений. В случае если полученные результаты признаны неудовлетворительными, следует пересмотреть исходные данные.
8. По найденным денежным затратам на проведение мероприятий рассчитываются достигаемые значения конечных показателей, которые соответствуют строкам, исключенным из матрицы D. Оценивается приемлемость тех из значений конечных показателей, которые не совпадают с планируемыми, поскольку именно эти запланированные значения приводили к несовместности системы. В случае, если полученные значения конечных показателей признаны неудовлетворительными, то следует пересмотреть принципы планирования (ограничения, желаемые конечные результаты).
К решению системы линейных уравнений также сводится и задача распределения по мероприятиям заданного общего объема денежных средств. Причем рекомендации по ее решению полностью совпадают с рассмотренными с той лишь разницей, что в систему добавляется еще одно линейное уравнение:
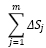
где ΔSΣ – заданный суммарный объем денежных средств.
Тогда система линейных уравнений (1.10), подлежащая решению, принимает следующий вид:
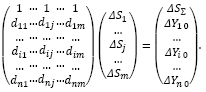
При реализации рассмотренных рекомендаций по решению этой системы первой строке матрицы (все единицы) в процессе ранжирования присваивается самая высокая важность. Эта строка должна быть базисной – она не должна исключаться, даже если система окажется несовместной.
Для решения систем линейных уравнений, имеющих единственное решение, существуют различные методы, достаточно полно представленные в математической литературе. Анализ, проведенный в настоящем исследовании, показал, что наиболее предпочтительным в рассматриваемом случае является метод Гаусса, основанный на приведении матрицы к треугольной [5].
Следует указать на существующие сложности в реализации рассмотренных рекомендаций по совершенствованию методов планирования бюджета, которые связаны с огромным объемом вычислений и необходимостью разработки и выбора достаточно эффективных алгоритмов. Эти сложности связаны с:
- определением базисных строк и столбцов матрицы с учетом их ранжирования;
- решением системы линейных уравнений, при большом количестве уравнений и неизвестных;
- учетом точности расчетов.
Особую актуальность этот вопрос имеет в отношении расчета определителей матриц, особенно если выполняется анализ, содержащий сравнение определителя матрицы с нулем (например, при определении ранга матрицы, базисных строк и столбцов и др.). Из-за погрешностей расчетов и округления данных некоторый, по существу, равный нулю определитель при практическом вычислении таковым может не оказаться, что вызовет цепочку дальнейших некорректностей.
Разработка рекомендаций по решению задачи бюджетирования
путем сведения ее к задаче линейного программирования
К задачам линейного программирования, представляемым в формализованном виде математическими выражениями (3) и (4), сводятся задачи, при постановке которых, определяются целевые установки на оптимизацию какого-либо параметра. В задаче (3) минимизируется общий бюджет, в (4) – оптимизируется один из конечных показателей (минимизируется или максимизируется – в зависимости от сущности выбранного показателя). Ограничения в общем виде задаются равенствами или неравенствами типа «не меньше» и «не больше», в которые входят линейные (по отношению к искомым приращениям денежных средств) математические выражения, определяемые линейной моделью. Условия в виде неравенств могут содержать оба знака неравенства («<» и «>»). В линейном программировании строгие неравенства «<» и «>» не используются [7], так как при задаваемых ими ограничениях задача линейного программирования обычно не имеет решения (ибо точки экстремума, как доказывается в теории линейного программирования, располагаются на границе области, задаваемой неравенствами и потому обязательно должны обращать некоторые из неравенств в равенства). Для линейной функции и для линейных условий удается задачу нахождения экстремума решить (по крайней мере, теоретически) полностью за конечное (хотя, возможно, и очень большое – например, в экономике) число шагов [7]. Решением задачи является совокупность значений приращений денежных средств, определяемых на проведение каждого из планируемых мероприятий.
Для решения задач линейного программирования могут быть использованы многие существующие компьютерные программы – от простой на нынешний день программы Eureka до таких мощных пакетов, как MathCad и Mathematica, а также специализированных математических программ [5].
В основу решения задач линейного программирования ложится «симплекс- метод» [4]. Вопрос состоит лишь в том, в каком виде необходимо формулировать оптимизационную задачу для конкретной компьютерной программы.
Так, требованием некоторых программ является представление задачи в каноническом виде [2]: ограничения должны быть выражены только равенствами, а целевая функция должна минимизироваться. В других программах решается так называемая основная задача, при формулировании которой ограничения требуется выразить в виде неравенств типа «не больше» («<») [2].
Поэтому в зависимости от того, какой программный продукт используется, формальное представление задачи, возможно, придется преобразовать.
Следует отметить, что любое равенство можно записать в виде системы, состоящей из двух неравенств. Например, равенство вида
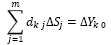
Эквивалентно, очевидно, следующей системе двух неравенств:
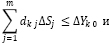
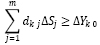
или
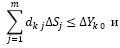
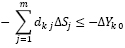
Поэтому систему условий произвольной задачи (3) линейного программирования, задаваемых в виде неравенств и (или) неравенств, всегда можно привести к системе неравенств, которая в общем случае примет следующий вид:
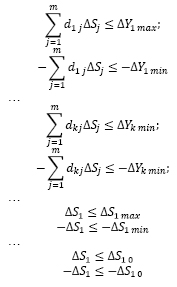
В данной системе все неравенства приведены к однообразному типу «не больше» («≤»).
В компьютерных программах, предназначенных для решения задач линейного программирования, все переменные обычно предполагаются неотрицательными. Есть программы, в которых такие ограничения не накладываются, но это бывает очень редко и, потому, часто условия неотрицательности даже не всегда в явном виде выписывают, предполагая их как бы наполняемыми по умолчанию. В случае, если необходимо избавиться от отрицательных переменных, обычно существующие переменные отображают в виде разности двух заведомо неотрицательных величин. Для задач (3)и (4) это целесообразно сделать, переходя от приращений средств к сумме денежных средств Sj выделяемых на проведение мероприятий:
Sj = Sj0 + ΔSj ,
где Sj0 – распределение денежных средств в предыдущем отчетном периоде, приведенных к стоимостным характеристикам, ожидаемым в планируемом периоде.
Следует отметить, что переход к новым переменным Sj даже желателен, т.к. нахождение именно этих величин и составляет суть решения задачи бюджетирования.
Тогда при замене переменной выражением ΔSj = Sj – Sj0, ограничения примут вид, типа
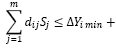
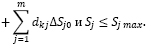
Если программа задачи линейного программирования требует записывать ограничения в виде равенств, то переход от неравенств к равенствам производится введением дополнительных переменных.
Так, неравенства (8) введением дополнителен переменных Zyi и Vxj преобразуются к равенствам
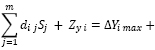
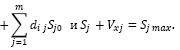
И неравенствам стандартного типа Zyi ≥ 0, Vxj ≥ 0.
Таким образом, от системы условий, задаваемых равенствами и неравенствами, можно перейти к системе равенств (точнее, к системе линейных алгебраических уравнений), дополненной системой стандартных неравенств – условий не отрицательности переменных. Именно к такому виду обычно приводятся условия канонической задачи линейного программирования во многих алгоритмах для их решения.
Если среди условий задачи имеются линейные равенства, то их при желании можно использовать для уменьшения числа переменных. Для этого надо с помощью этих уравнений выразить часть переменных через остальные величины и подставить эти выражения, как в оставшиеся условия, так и в целевую функцию.
Задача (4) имеет ту особенность, что ищется экстремум не общего бюджета, а показателя некоторого конечного результата при заданном общем бюджете. В такой постановке задача формулируется, когда задается общий бюджет при не определенных значениях некоторых конечных показателей. В качестве таких конечных показателей при сведении задачи бюджетирования к задаче линейного программирования целесообразно брать те, которые по каким-то соображениям приняты наиболее важными.
Взаимовлияние системы и среды представляет собой непрерывный процесс. Однако его интенсивность различна. Особенно высокой она становится тогда, когда система выступает в роли основы, авангарда, первой осуществляя прорыв, отражающий в своей области назревшие объективные потребности. Если же развитие конкретной системы отстает по темпам от изменения среды, то доминирующим элементом их взаимодействия становится последняя. Адаптация среды к системе, как правило, происходит гораздо интенсивнее, чем обратный процесс, поскольку в этом случае воздействие, даже чисто количественное, является более всесторонним, массированным и соответственно глубоким. При этом чем больше изменения произошли в институциональной среде, тем больше ее преобразующая сила. Нередко в ходе исторического развития система и среда, находящиеся во взаимодействии, как бы меняются местами. На одном этапе система, осуществившая прорыв, превращается в определяющий источник импульсов, подстегивающих изменения в среде. На другом – пришедшая в движение среда обгоняет в своем развитии систему и, в свою очередь, трансформирует ее в соответствии со своим обликом. Социально-экономические системы (в качестве примера мы рассматриваем налоговую) относятся к классу сложных саморазвивающихся целевых систем, моделирование которых представляет большие трудности [1].
Библиографическая ссылка
Башашкина Г.Ю. МЕТОДИКА ЭКОНОМИКО-МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ НА ОСНОВЕ ИСПОЛЬЗОВАНИЯ ЛИНЕЙНОЙ МОДЕЛИ БЮДЖЕТИРОВАНИЯ // Вестник Алтайской академии экономики и права. 2020. № 11-2. С. 170-178;URL: https://vaael.ru/ru/article/view?id=1408 (дата обращения: 11.03.2026).
DOI: https://doi.org/10.17513/vaael.1408

