Научный журнал

Вестник Алтайской академии экономики и права

Print ISSN 1818-4057

Online ISSN 2226-3977

Перечень ВАК

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Горский М.А. 1 Сокерин П.О. 1 Юркевич Е.А. 1

---

1 Институт цифровой экономики и информационных технологий, Российский экономический университет им. Г.В. Плеханова

В статье представлены новые результаты, полученные авторами в рамках продолжения работы по тематике более ранней (опубликованной) статьи. Эти результаты включают: постановки задач и математические модели формирования оптимальных портфелей финансовых активов в постановках Г. Марковица и В. Шарпа с учетом ограничения по ликвидности (в более ранней работе это ограничение не использовалось). Представлены варианты оптимальных портфелей, рассчитанных для инвесторов умеренно-агрессивного типа с различными объемами инвестиционного капитала. Приведены отличия полученных портфелей по структуре и показателям доходности и риска. В предыдущей работе обоснован вывод о преимуществах использования для условий развивающегося российского фондового рынка «классической» задачи портфельного инвестирования в постановке Г. Марковица, позволяющей более адекватно отразить несовершенства институциональных механизмов его функционирования. В данной работе показано, что этот результат остается справедливым и для случая, когда в задаче портфельного инвестирования, рассматриваемой в постановках Г. Марковица и В. Шарпа, дополнительно к критериям доходности и риска предлагается учитывать и критерий ликвидности отдельно ценной бумаги и, в целом, инвестиционного портфеля.

Статья в формате PDF

0 KB

инвестиционный портфель

структура портфеля

теория оптимального портфеля

неинституциональный инвестор

умеренно-агрессивный инвестор

развивающийся фондовый рынок

модель портфеля в постановке г. марковица

модель портфеля в постановке в. шарпа

1. Грибов А. Ф. Болдин Б.С. Методы и модели стратегического управления коммерческими банками. М.: Изд. дом Академии Естествознания, 2015. 226 с.

2. Максимов Д.А., Халиков М.А. Концепция и теоретические основы управления производственной сферой предприятия в условиях неопределенности и риска // Международный журнал прикладных и фундаментальных исследований. 2015. № 10-4. С. 711-719.

3. Халиков М.А., Хечумова Э.А., Щепилов М.В. Модели и методы выбора и оценки эффективности рыночной и внутрифирменной стратегий предприятия / под общ. ред. проф. Халикова М.А. М.: Коммерческие технологии, 2015. 595 с.

4. Instefjord N. Investment management. Undergraduate study in Economics, Management, Finance and the Social Sciences. London: University of London, 2016. 126 р.

5. Брейли Р, Майерс С. Принципы корпоративных финансов. М.: Олимп-Бизнес. 2008.

6. Зельцер М.Б. Оценка эффективности управления паевыми инвестиционными фондами: автореф. дис. … канд. экон. наук. Н., 2006. 163 с.

7. Миркин Я.М. Ценные бумаги и фондовый рынок. Профессиональный курс в Финансовой Академии при Правительстве РФ. М.: Перспектива, 1995. 488 с.

8. Markowitz H.M. Portfolio Selection: Efficient Diversification of Investment. Wiley. New York, 1959.

9. Sharp W. Simplified model for portfolio analysis // Management Sciences. 1963. Vol. 9. № 2.

10. Tobin J. Liquidity Preference as Behavior Towards Risk // Review of Economic Studies. 1958. Vol. 26. № 1.

11. Tobin J. The Theory of Portfolio Selection. The Theory of Interest Rates // ed. By Hahn F. and Brechlin. London: Macmillan and Co., 1965. P. 3-51.

12. Антиколь А.М. Критерий ликвидности финансовых активов в задачах портфельного инвестирования // Финансовый менеджмент. 2012. №5. С. 94-101.

13. Быстрова Д.А., Рязанов М.А. Информационно-алгоритмическое обеспечение оптимального управления портфелем финансовых активов неинституционального инвестора // Фундаментальные исследования. 2017. № 9-1. С. 141-146.

14. Горощенко В.Б. Развитие инвестиционных механизмов российского фондового рынка: автореф. дис. … канд. экон. наук. М., 2015. 24 с. [Электронный ресурс] URL: https://dlib.rsl.ru/viewer/01005563332#?page=1&view=list (дата обращения: 12.02.2020).

15. Кухаренко А. Ю., Халиков М. А. Выбор портфеля неинституционального инвестора с использованием критерия Вальда – Сэвиджа // Фундаментальные исследования, № 5, 2019. С. 62-68.

16. Халиков М.А., Максимов Д.А. Особенности моделей управления инвестиционным портфелем неинституционального инвестора-агента российского фондового рынка // Фундаментальные исследования. 2015. № 2-14. С. 3136-3145.

17. Хасанов А.С. Об особенностях алгоритмов решения задач линейного программирования с неограниченными областями допустимых решений // Вестник Московского государственного областного университета. Серия: Физика-Математика. 2017. № 1. С. 113-123. 

18. Федеральный закон РФ от 22.04.1996. № 39-ФЗ «О рынке ценных бумаг».

19. Федеральный закон РФ от 25.02.1999 N 39-ФЗ «Об инвестиционной деятельности в Российской Федерации, осуществляемой в форме капитальных вложений».

20. Официальный сайт брокерской компании «Финам» [Электронный ресурс] URL: https://www.finam.ru (дата обращения: 05.02.2020).

21. Официальный сайт информационно-аналитического агентства “Investfunds” [Электронный ресурс] URL: https://investfunds.ru (дата обращения: 05.02.2020).

22. Официальный сайт информационно-аналитического агентства “Investopedia” [Электронный ресурс] URL: https://www.investopedia.com (дата обращения: 07.02.2020).

23. Официальный сайт Международного Валютного Фонда. [Электронный ресурс] URL: https://www.imf.org/external/index.htm (дата обращения: 07.02.2020).

24. Официальный сайт Московской биржи [Электронный ресурс]. URL: https://www.moex.com/ (дата обращения: 05.02.2020).

25. Официальный сайт Центрального Банка РФ [Электронный ресурс]. URL: https://www.cbr.ru (дата обращения: 26.02.2020).

26. Сайт информационного ресурса “World-exchanges” [Электронный ресурс]. URL: https://www.world-exchanges.org (дата обращения: 25.05.2019).

27. Сайт информационного ресурса “Yahoo finance” [Электронный ресурс]. URL: https://finance.yahoo.com/ (дата обращения: 25.05.2019).

Введение

Эта статья является прямым продолжением работы Горского М.А., Сокерина П.О. и Юркевич Е.А. «Особенности применения моделей оптимальных портфелей на развивающихся фондовых рынках», опубликованной в «Вестнике Алтайской академии экономики и права», № 5-1, стр.40-52 и содержит краткое изложение приведенных в ней постановок задач и новых результатов, полученных авторами по заявленной тематике.

Это позволяет лишь кратко напомнить основные положения более ранней публикации и основное внимание сосредоточить на новых результатах.

На сегодняшний день проблематика оптимального управления портфелями ценных бумаг непрофессиональных агентов фондовых рынков достаточно актуальна, так как именно эта группа инвесторов составляет значительную долю участников российского фондового рынка (инвесторы этой группы обладают достаточными объемами свободных денежных средств для совершения рыночных сделок с целью получения дохода от неосновного для них вида деятельности).

Эти инвесторы для совершения биржевых операций использует различные по сложности и функционалу математические модели и компьютерные программы формирования портфелей и сопровождения сделок с финансовыми активами с учетов выбранной инвестиционной стратегии и параметров рынка ценных бумаг. Эти инструменты помогают непрофессиональным инвесторам принимать решения относительно портфельных инвестиций, учитывая особенности и уровень развитости институциональных механизмов функционирования рынка, характеризуемого показателями капитализации и ликвидности, величинами вход-выходных барьеров и трансакционных издержек биржевых операций.

Стоит отметить, что российский развивающийся фондовый рынок характеризуется несовершенством рыночных механизмов, низкой капитализацией, невысокой ликвидностью, что предполагает при совершении рыночных сделок учета расширенного набора показателей качества финансовых активов. Важным в условиях низкого институционального развития российского фондового рынка фактором выбора инвестиционной стратегии неинституционального (в значении непрофессионального) инвестора является ликвидность финансовых инструментов, включаемых в портфель, на «бытовом» уровне понимаемая как возможность обратной конвертации в наличные деньги в ограниченные сроки и без существенных (с позиции инвестора) потерь капитала. Именно по этой причине необходимо при формировании портфеля учитывать не только показатели доходности активов и риска вложений, но и уровень ликвидности, и долю ликвидных активов в портфеле.

Методологическая основа исследования

Методологическую основу работы составили труды отечественных и зарубежных ученых и исследователей-практиков по проблематике разработки и совершенствования экономико-математических моделей, методов и численных алгоритмов формирования и управления портфелями финансовых активов профессиональных и непрофессиональных игроков фондового рынка, в том числе:

- теории и практике инвестирования на совершенных и несовершенных в институциональном отношении рынках капитала [1,2,3,4];

- «классической» портфельной теории и практике инвестирования на развитых рынках катила [5,6,7,8,9,10,11];

- математическим моделям, численным методам и инструментальным средствам оптимального управления портфельными инвестициями на развивающихся фондовых рынках, в том числе, и российском [12,13,14,15,16];

- численных методов решения задач линейной и нелинейной оптимизации в непрерывной и дискретной постановках [17];

- правового сопровождения инвестиционной деятельности на российском фондовом рынке [18,19].

Статистическая и информационная база исследования сформированы на основе данных официальных сайтов российских фондовых бирж, Центрального банка, ряда УК и брокеров Cbonds и Финам за период: вторая половина2018 – конец 2019, начало 2020 гг. [20,21,22,23,24,25,26,27].

Цель исследования – сопоставительный анализ инструментария моделей Г. Марковица и У. Шарпа в приложении к задаче формирования оптимального портфеля финансовых активов неинституционального инвестора-агента развивающегося российского фондового рынка с учетом расширенного набора показателей качества активов, включающего наряду с доходностью и риском ликвидность ценной бумаги.

Результаты исследования и их обсуждение

В работе рассмотрены модели оптимальных портфелей в постановках Г. Марковица и В. Шарпа с учетом показателя ликвидности для группы умеренно-агрессивных инвесторов (преобладающая группа инвесторов – непрофессиональных участников российского фондового рынка), который ориентируется на долгосрочные вложения и устойчивый рост инвестиционного капитала. Данная категория инвесторов допускает наличие в портфеле ценных бумаг среднего уровня риска. Основными инструментами инвестирования являются ценные бумаги крупных и средних, но надежных и длительно работающих на рынке компаний, также в портфеле ценных бумаг умеренно-агрессивного инвестора может присутствовать незначительная доля государственных ценных бумаг.

В перечень ценных бумаг для формирования портфеля на 3 января 2020 г. включены ценные бумаги, входящие в базу расчета индекса РТС, взвешенного по рыночной капитализации (free-float), композитные индексы российского фондового рынка, включающие наиболее ликвидные акции крупнейших и динамично развивающихся российских эмитентов, виды экономической деятельности которых относятся к основным секторам экономики. Каждой ценной бумаге был присвоен номер группы ликвидности в зависимости от среднего значения ликвидности данного актива (табл. 1) (здесь и ниже автор использовал данные информационных сайтов, представленных в списке литературных источников и приведенных выше при описании методологической основы исследования).

Приведем модель оптимального инвестиционного портфеля Г. Марковица с критерием на максимум среднемесячной доходности и ограничением по ликвидности.

Ниже при описании модели (1) будем использовать следующие обозначения переменных и параметров:

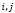– акции из пула финансовых инструментов инвестора;

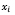– количество акций i-го эмитента в портфеле (целое положительное число);

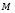– бюджет инвестора;

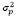– уровень риска (волатильности) портфеля за период владения ценными бумагами;

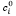– котировка акции i-го эмитента в момент формирования портфеля;

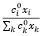– доля i-го актива в целочисленном портфеле;

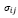– ковариация i-го и j-го активов в портфеле;

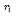– средняя ожидаемая доходность i-го актива;

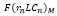– функция модели Марковица от доходности и ликвидности;

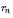– нормированная доходность i-го актива;

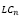– нормированная ликвидность i-го актива;

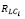– ранг ликвидности i-го актива;

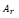– весовой коэффициент функции доходности.

Таблица 1

Перечень ценных бумаг для формирования опорного портфеля инвестора умеренно-агрессивного типа

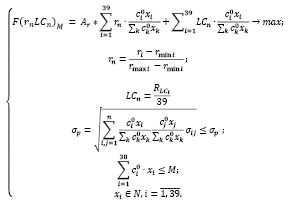(1)

Приведем модель оптимального инвестиционного портфеля Г. Марковица с группировкой активов по ликвидности. Критерий оптимальности – максимум среднемесячной доходности с учетом ликвидности, с использованием весовых коэффициентов ликвидности ценных бумаг.

Ниже при описании модели (2) будем использовать следующие обозначения переменных и параметров:

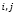– акции из пула финансовых инструментов инвестора;

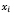– количество акций i-го эмитента в портфеле (целое положительное число);

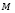– бюджет инвестора;

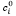– котировка акции i-го эмитента в момент формирования портфеля;

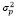– уровень риска (волатильности) портфеля за период владения ценными бумагами;

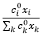– доля i-го актива в целочисленном портфеле;

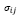– ковариация i-го и j-го активов в портфеле;

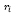– средняя ожидаемая доходность i-го актива;

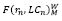– функция модели Марковица от доходности и ликвидности с использованием весовых коэффициентов ликвидности;

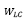– весовой коэффициент группа ликвидности i-го актива,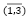

Приведем модель оптимального инвестиционного портфеля В. Шарпа с группировкой активов по ликвидности. Критерий оптимальности – максимум среднемесячной доходности, деленной на риск с учетом ликвидности, с использованием весовых коэффициентов ликвидности ценных бумаг.

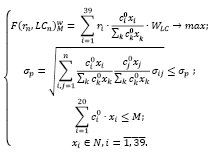(2)

Ниже при описании модели (3) будем использовать следующие обозначения переменных и параметров:

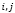– акции из пула финансовых инструментов инвестора;

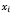– количество акций i-го эмитента в портфеле (целое положительное число);

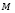– бюджет инвестора;

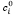– котировка акции i-го эмитента в момент формирования портфеля;

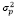– уровень риска (волатильности) портфеля за период владения ценными бумагами;

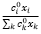– доля i-го актива в целочисленном портфеле;

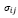– ковариация i-го и j-го активов в портфеле;

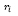– средняя ожидаемая доходность i-го актива;

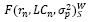– функция модели Шарпа от доходности, риска и ликвидности с использованием весовых коэффициентов ликвидности.

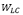– весовой коэффициент группа ликвидности i-го актива, .

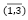Примечание. В качестве средней ожидаемой доходности i-го актива рассматривается средняя месячная доходность ценной бумаги за период с 1 октября 2017 г. по 31 декабря 2019 г.

Построим модель (4) оптимального портфеля Марковица для умеренно-агрессивного инвестора с учетом ликвидности активов с небольшим бюджетом (500000 руб.). Критерий оптимальности – максимум среднемесячной доходности с учетом ликвидности.

Структура и характеристики оптимального портфеля представлены в таблицах 2 и 3.

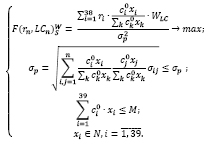(3)

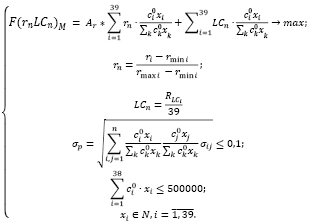(4)

Таблица 2

Структура оптимального портфеля, построенного по модели Марковица, с учетом фактора ликвидности и ограничением на бюджет 500000 руб.

Таблица 3

Характеристики оптимального портфеля, построенного по модели Марковица, с учетом фактора ликвидности и ограничением на бюджет 500000 руб.

Таблица 4

Структура оптимального портфеля, построенного по модели Марковица, с группировкой активов по ликвидности и ограничением на бюджет 500000 руб.

Построим модель (5) оптимального портфеля Марковица с группировкой активов по ликвидности для умеренно-агрессивного инвестора с небольшим бюджетом (500000 руб.). Критерий оптимальности – максимум среднемесячной доходности с учетом ликвидности, с использованием весовых коэффициентов ликвидности ценных бумаг.

Структура и характеристики оптимального портфеля представлены в таблицах 4 и 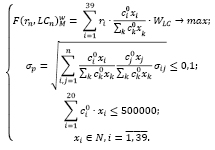5.

(5)

Таблица 5

Характеристики оптимального портфеля, построенного по модели Марковица, с группировкой активов по ликвидности и ограничением на бюджет 500 000 руб.

Таблица 6

Структура оптимального портфеля, построенного по модели Шарпа, с группировкой активов по ликвидности и ограничением на бюджет 500000 руб.

Таблица 7

Характеристики оптимального портфеля, построенного по модели Шарпа, с группировкой активов по ликвидности и ограничением на бюджет 500000 руб.

Построим модель (6) оптимального портфеля В. Шарпа с группировкой активов по ликвидности для умеренно-агрессивного инвестора с небольшим бюджетом (500000 руб.). Критерий оптимальности – максимум среднемесячной доходности, деленной на риск, с учетом ликвидности, с использованием весовых коэффициентов ликвидности ценных бумаг.

Структура и характеристики оптимального портфеля представлены в таблицах 6 и 7.

Сравним структуры полученных портфелей. В оптимальный портфель, построенный по модели Г. Марковица с учетом фактора ликвидности, входят 940 привилегированных акций ПАО «Татнефть» имени В.Д. Шашина. В портфель, построенный по модели Марковица с группировкой активов по ликвидности, входят 16578 обыкновенных акций ПАО «Сургутнефтегаз». В оптимальный портфель, построенный по модели Шарпа, входят 47566 обыкновенных акций ПАО «Московский кредитный банк», 6 депозитарных расписок иностранного эмитента на акции Икс 5 Ритейл Груп Н.В., 278 обыкновенных акций ПАО «Газпром», 28083 обыкновенных акций ПАО «Интер РАО ЕЭС», 18 обыкновенных акций ПАО «Нефтяная компания «ЛУКОЙЛ», 86 акций иностранного эмитента Юнайтед Компани РУСАЛ плс.

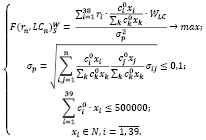(6)

Инвестиции в портфель, построенный по модели Марковица с учетом фактора ликвидности, составили 499 537 руб., что на 1,17% больше, чем инвестиции в портфель по модели Г. Марковица с группировкой активов по ликвидности и на 0,05% больше, чем инвестиции в портфель, построенный по модели Шарпа с группировкой активов по ликвидности. В то же время наибольшая среднемесячная доходность наблюдается для портфеля, построенного по модели Г. Марковица с учетом фактора ликвидности (3,36%), что на 1,05% больше чем среднемесячная доходность портфеля, построенного по модели Марковица с группировкой активов по ликвидности, и на 1,82% больше, чем среднемесячная доходность портфеля, построенного по модели У. Шарпа с группировкой активов по ликвидности. Наименьшее значения показателя среднемесячной доходности, деленной на риск за период владения ценными бумагами, наблюдается для портфеля, построенного по модели Марковица с группировкой активов по ликвидности (0,296). Полученные портфели значительно отличаются по структуре.

Построим модель (7) оптимального портфеля Марковица для умеренно-агрессивного инвестора с учетом ликвидности активов со средним бюджетом (2 000 000 руб.). Критерий оптимальности – максимум среднемесячной доходности с учетом ликвидности.

Структура и характеристики оптимального портфеля представлены в таблицах 8 и 9.

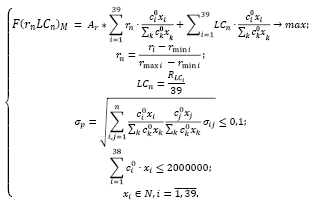(7)

Таблица 8

Структура оптимального портфеля, построенного по модели Марковица, с учетом фактора ликвидности и ограничением на бюджет 2000000 руб.

Таблица 9

Характеристики оптимального портфеля, построенного по модели Марковица, с учетом фактора ликвидности и ограничением на бюджет 2000000 руб.

Таблица 10

Структура оптимального портфеля, построенного по модели Марковица, с группировкой активов по ликвидности и ограничением на бюджет 2000000 руб.

Построим модель (8) оптимального портфеля Марковица с группировкой активов по ликвидности для умеренно-агрессивного инвестора со средним бюджетом (2000000 руб.). Критерий оптимальности – максимум среднемесячной доходности с учетом ликвидности, с использованием весовых коэффициентов ликвидности ценных бумаг.

Структура и характеристики оптимального портфеля представлены в таблицах 10 и 11.

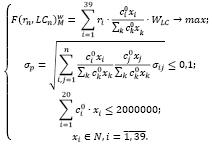(8)

Таблица 11

Характеристики оптимального портфеля, построенного по модели Марковица, с группировкой активов по ликвидности и ограничением на бюджет 2000000 руб.

Таблица 12

Структура оптимального портфеля, построенного по модели Шарпа, с группировкой активов по ликвидности и ограничением на бюджет 2000000 руб.

Построим модель (9) оптимального портфеля Шарпа с группировкой активов по ликвидности для умеренно-агрессивного инвестора со средним бюджетом (2000000 руб.). Критерий оптимальности – максимум среднемесячной доходности, деленной на риск, с учетом ликвидности, с использованием весовых коэффициентов ликвидности ценных бумаг.

Структура и характеристики оптимального портфеля представлены в таблицах 12 и 13.

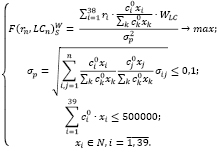(9)

Таблица 13

Характеристики оптимального портфеля, построенного по модели Шарпа, с группировкой активов по ликвидности и ограничением на бюджет 2000000 руб.

Сравним структуры полученных портфелей. В оптимальный портфель, построенный по модели Г. Марковица с учетом фактора ликвидности, входят 3763 привилегированных акций ПАО «Татнефть» им. В.Д. Шашина. В портфель, построенный по модели Марковица с группировкой активов по ликвидности, входят 67152 обыкновенных акций ПАО «Сургутнефтегаз». В оптимальный портфель, построенный по модели Шарпа, входят 190828 обыкновенных акций ПАО «Московский кредитный банк», 25 депозитарных расписок иностранного эмитента на акции Икс 5 Ритейл Груп Н.В., 1102 обыкновенных акций ПАО «Газпром», 113083 обыкновенных акций ПАО «Интер РАО ЕЭС», 73 обыкновенных акций ПАО «Нефтяная компания «ЛУКОЙЛ», 86 акций иностранного эмитента Юнайтед Компани РУСАЛ плс.

Инвестиции в портфель, построенный по модели Марковица с учетом фактора ликвидности, составили 1999742 руб., что на 0,011% меньше, чем инвестиции в портфель, построенный по модели Г. Марковица с группировкой активов по ликвидности, и на 0,0127% меньше, чем инвестиции в портфель, построенный по модели Шарпа с группировкой активов по ликвидности. В то же время наибольшая среднемесячная доходность – у портфеля, построенного по модели Марковица с учетом фактора ликвидности (3,35%), что на 1,05% больше чем среднемесячная доходность портфеля, построенного по модели Г. Марковица с группировкой активов по ликвидности, и на 1,8% больше, чем среднемесячная доходность портфеля, построенного по модели Шарпа с группировкой активов по ликвидности. Наименьшее значения показателя среднемесячной доходности, деленной на риск за период владения ценными бумагами, наблюдается для портфеля, построенного по модели Марковица с группировкой активов по ликвидности (0,296). Полученные портфели значительно различаются по структуре. Однако они идентичны портфелям, полученными для бюджета, равного 500000 руб.

Построим модель (10) оптимального портфеля Марковица для умеренно-агрессивного инвестора с учетом ликвидности активов с большим бюджетом (10000000 руб.). Критерий оптимальности – максимум среднемесячной доходности с учетом ликвидности.

Структура и характеристики оптимального портфеля представлены в таблицах 14 и 15.

Таблица 14

Структура оптимального портфеля, построенного по модели Марковица, с учетом фактора ликвидности и ограничением на бюджет 10000000 руб.

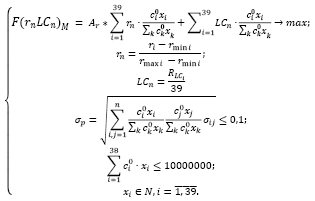(10)

Таблица 15

Характеристики оптимального портфеля, построенного по модели Марковица, с учетом фактора ликвидности и ограничением на бюджет 10000000 руб.

Построим модель (11) оптимального портфеля Марковица с группировкой активов по ликвидности для умеренно-агрессивного инвестора с большим бюджетом (10000000 руб.). Критерий оптимальности – максимум среднемесячной доходности с учетом ликвидности, с использованием весовых коэффициентов ликвидности ценных бумаг.

Структура и характеристики оптимального портфеля представлены в таблицах 16 и 17.

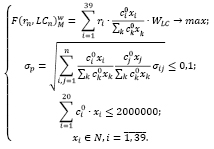(11)

Таблица 16

Структура оптимального портфеля, построенного по модели Марковица, с группировкой активов по ликвидности и ограничением на бюджет 10000000 руб.

Таблица 17

Характеристики оптимального портфеля, построенного по модели Марковица, с группировкой активов по ликвидности и ограничением на бюджет 10000000 руб.

Построим модель (12) оптимального портфеля Шарпа с группировкой активов по ликвидности для умеренно-агрессивного инвестора с большим бюджетом (10000000 руб.). Критерий оптимальности – максимум среднемесячной доходности, деленной на риск, с учетом ликвидности, с использованием весовых коэффициентов ликвидности ценных бумаг.

Структура и характеристики оптимального портфеля представлены в таблицах 18 и 19.

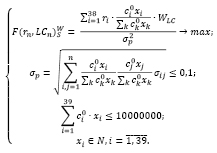(12)

Таблица 18

Структура оптимального портфеля, построенного по модели Шарпа, с группировкой активов по ликвидности и ограничением на бюджет 10000000 руб.

Таблица 19

Характеристики оптимального портфеля, построенного по модели Шарпа, с группировкой активов по ликвидности и ограничением на бюджет 10000000 руб.

Сравним структуры полученных портфелей. В оптимальный портфель, построенный по модели Г. Марковица с учетом фактора ликвидности, входят 18817 привилегированных акций ПАО «Татнефть» имени В.Д. Шашина. В портфель, построенный по модели Марковица с группировкой активов по ликвидности, входят 311812 обыкновенных акций ПАО «Сургутнефтегаз». В оптимальный портфель, построенный по модели Шарпа, входят 954603 обыкновенных акций ПАО «Московский кредитный банк», 125 депозитарных расписок иностранного эмитента на акции Икс 5 Ритейл Груп Н.В., 5498 обыкновенных акций ПАО «Газпром», 566507 обыкновенных акций ПАО «Интер РАО ЕЭС», 363 обыкновенных акций ПАО «Нефтяная компания «ЛУКОЙЛ», 86 акций иностранного эмитента Юнайтед Компани РУСАЛ плс.

Инвестиции в портфель, построенный по модели Марковица с учетом фактора ликвидности, составили 9999772 руб., что на 7,67% больше, чем инвестиции в портфель, построенный по модели Г. Марковица с группировкой активов по ликвидности, и на 0,152% больше, чем инвестиции в портфель, построенный по модели. Шарпа с группировкой активов по ликвидности. В то же время наибольшая среднемесячная доходность наблюдается для портфеля, построенного по модели Марковица с учетом фактора ликвидности (3,35%), что на 1,05% больше чем среднемесячная доходность портфеля, построенного по модели Г. Марковица с группировкой активов по ликвидности и на 1,8% больше чем среднемесячная доходность портфеля, построенного по модели Шарпа с группировкой активов по ликвидности. Наименьшее значения показателя среднемесячной доходности, деленной на риск за период владения ценными бумагами, наблюдается для портфеля, построенного по модели Марковица с группировкой активов по ликвидности (0,296). Полученные портфели значительно отличаются по структуре. Следует также отметить, что полученные портфели по структуре идентичны портфелям, полученным для ограничения бюджета, равного 500000 руб., и для ограничения, равного 2000000 руб.

Заключение

Анализ состава и структуры оптимальных портфелей для умеренно-агрессивных инвесторов – основной группы непрофессиональных инвесторов – агентов российского фондового рынка, построенных по моделям Марковица и Шарпа, показал их существенное различие, что отмечено и в предыдущей работе. Дополнительные исследования показали, что учет в моделях ограничения на ликвидность портфеля увеличивает различия в структуре оптимальных портфелей. Также показано, что оптимальные портфели с учетом ограничения на ликвидность, сохраняют структуру для различных уровней инвестиционного бюджета. Таким образом, выбор модели портфеля – наиболее значимый аспект портфельного инвестирования на развивающимся фондовом рынке.

Библиографическая ссылка