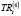Эта статья является прямым продолжением работы Димитриева А.М. «Математическое моделирование внутрифирменных денежных потоков интегрированной производственной структуры», опубликованной в «Вестнике Алтайской академии экономики и права» [15] и содержит изложение постановок задач и новых результатов, полученных авторами по заявленной тематике.
Это позволяет лишь кратко напомнить основные положения более ранней пуьликации и основное внимание сосредоточить на новых результатах.
На сегодняшний день проблематика оптимального управления денежными потоками предприятия – независимого агента рынка достаточно широко представлена в работах отечественных и зарубежных исследователей. Из последних публикаций на эту тему отметим работы профессора Халикова М.А. и его учеников [22–24, 26], в которых предложена концепция математического моделирования динамики денежных потоков предприятия с учетом как внутренних условий и ограничений его производственной и финансовой сферы, так и особенностей формирования капитала, авансируемого в затраты производственной и инвестиционной деятельности, расчета и выплаты налогов и пр. обременений [15].
Что же касается крупных производственных структур и холдингов, то отмеченная проблематика, весьма актуальная для них, исследована недостаточно. Фрагментарно она присутствует в монографии С.В. Бельченко, М.А. Халикова, М.В. Щепилова [10]. Общая постановка задачи моделирования внутрифирменных денежных потоков интегрированной группы предприятий приведена в работах автора и М.А. Халикова [3, 24]. Таким образом, данная работа претендует стать одной из первых исследований по заявленной проблематике.
Цель исследования – продолжение работ по созданию и адаптация экономико-математического инструментария моделей и методов выбора оптимального по экономическому критерию варианта управления внутрифирменными денежными потоками интегрированной группы предприятий с учетом приоритетов рыночной стратегии управляющей компании и структурных подразделений в ее составе, производственно-технологических и финансово-ресурсных ограничений совместной деятельности предприятий ИГП в операционной и инвестиционной сферах.
Материал и методы исследования
Методологическую основу исследования составили труды отечественных и зарубежных учёных по проблемам внутрифирменного управления, оценки эффективности и оптимизации рыночной деятельности крупных промышленных корпораций и холдингов – работы И.Ф. Алешиной [1,2], Г.Б. Клейнера [17], А. Грибова и Д.А. Максимова [12–14], В.О. Ивановой [16], М.А. Халикова и его учеников [19–24, 26, 29]. Автор использовал известный материал по моделям функции «выпуск – затраты», в том числе и в неоклассическом варианте, представленный в работах Г.Б. Клейнера [17], В.А. Колемаева [18], А.М. Антиколь, Д.А. Безухова, М.А. Никифоровой и М.А. Халикова [4, 8, 9, 27]. Проблематика оценки средневзвешенной цены капитала и выбора ставки дисконтирования, используемой в практических расчетах, представлена в работах К.В. Анциборко Д.А. Безухова, П.С. Емельянова, Д.А. Максимова, У.М. Шабалиной, М.А. Халикова [5, 25, 28], Автор использовал также результаты более ранних работ по динамической оптимизации денежных потоков предприятия, представленные в источниках [7, 8]. В оценках перспектив использования тех или иных численных методов решения рассматриваемой оптимизационной задачи автор ссылается на работы М. Аоки [6], М.А. Горского [11], М.А. Халикова [22].
Результаты исследования и их обсуждение
Напомним, что в цитируемой работе [15] рассматривается постановка задачи моделирования внутрифирменных денежных потоков интегрированной группы предприятий. Модель задается набором соотношений (1-30) приведенных в указанной статье.
Отметим, что численный метод решения динамической задачи, описываемой этими соотношениями может быть основан на общей идеи метода динамического программирования Р. Беллмана [11] и метода решения нелинейных дискретных задач с использованием схемы локальной оптимизации решения задачи линейной непрерывной оптимизации, предположенной М.А. Халиковым [4].
Эмпирические исследования динамики денежных потоков интегрированной группы предприятий в более ранней работе проводились на следующем примере:
– в ИГП входят 5 СБЕ 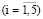 индекс «6» предназначен для управляющей компании;
индекс «6» предназначен для управляющей компании;
– примем за горизонт планирования денежных потоков ИГП временной интервал, включающий десять последовательных производственно-коммерческих циклов для каждой из пяти СБЕ: t = 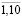 . Также будем считать, что внутренние и внешние условия деятельности УК и структурных подразделений холдинга, рыночные цены на продукцию и ставки кредитных организаций на этом горизонте неизменны: ci(1), Pt(i) , dt(i) , ρt(УК) = const;
. Также будем считать, что внутренние и внешние условия деятельности УК и структурных подразделений холдинга, рыночные цены на продукцию и ставки кредитных организаций на этом горизонте неизменны: ci(1), Pt(i) , dt(i) , ρt(УК) = const;
– исходные данные, характеризующие производственную сферу СБЕ моделируемой ИГП, представлены в следующей таблице (табл. 1);
– объем Ω0 централизованного инвестиционного фонда холдинга на конец нулевого временного интервала примем равным 100 ед.;
– экзогенные параметры ставок кредитных организаций по кредитам и депозитам юридических лиц примем неизменными на выбранном горизонте: ρt = 0,18; dt(i) = 0,16; ρt(УК) = 0,06 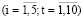 ; τ = 0,2;
; τ = 0,2;
– сделаем следующее предположение: на выбранном горизонте t = 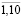 управляющая компания проводит политику стимулирования производственной активности первой СБЕ, отличающейся относительно невысоким масштабом выпуска, перечисляя остальным СБЕ равные доли трансфертных платежей. На протяжении десяти временных интервалов направлять на внутрифирменные трансферты 60 % от объема накопленного централизованного инвестиционного фонда холдинга:
управляющая компания проводит политику стимулирования производственной активности первой СБЕ, отличающейся относительно невысоким масштабом выпуска, перечисляя остальным СБЕ равные доли трансфертных платежей. На протяжении десяти временных интервалов направлять на внутрифирменные трансферты 60 % от объема накопленного централизованного инвестиционного фонда холдинга: 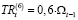 (t = 1, … ,10), которые распределять в соответствии с долями:
(t = 1, … ,10), которые распределять в соответствии с долями: 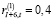 (t =
(t = 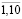 );
); 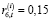 (i =
(i = 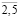 ; t =
; t = 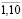 );
);
– для оценки влияния на эффективность производственной сферы СБЕ в составе холдинга в условиях общей политики дивидендных выплат снизим долю отчислений первых двух СБЕ в централизованный инвестиционный фонд, определив значения долей отчислений трех других СБЕ на одинаковом постоянном уровне: 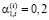 (i =
(i = 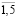 ; t =
; t = 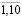 );
); 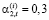 (i = 1,2; t =
(i = 1,2; t = 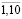 );
); 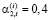 (i = 3,4,5; t =
(i = 3,4,5; t = 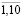 );
);
– эффективность рыночной деятельности подразделений интегрированной группы на временных интервалах t = 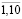 проводятся в соответствии с абсолютными и относительными показателями финансового результата и рентабельности осуществленных затрат:
проводятся в соответствии с абсолютными и относительными показателями финансового результата и рентабельности осуществленных затрат: 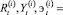
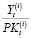 , (i =
, (i = 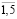 ; t =
; t = 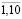 ).
).
В качестве показателя эффективности деятельности управляющей компании будем рассматривать объем Ωt централизованного инвестиционного фонда холдинга и среднюю отдачу внутрифирменных трансфертов в результатах производственной деятельности структурных подразделений: 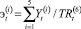 , (t =
, (t =  ).
).
Таблица 1
Исходные данные-характеристики производственной сферы моделируемой ИГП
|
Номер СБЕ (i) |
Степень однородности γi функции «затраты-выпуск» |
Удельные затраты ci(1) рабочего капитала i-й СБЕ |
Средневзвешенная цена Pt(i) продукции i-й СБЕ |
Начальный уровень РКн(i) рабочего капитала i-й СБЕ |
|
1 |
0,6 |
1,2 |
2,0 |
136,0 |
|
2 |
0,75 |
1,3 |
2,1 |
142,0 |
|
3 |
0,8 |
1,32 |
2,2 |
144,0 |
|
4 |
0,83 |
1,33 |
2,2 |
144,0 |
|
5 |
0,85 |
1,4 |
2,2 |
146,0 |
Расчеты динамики денежных потоков рассматриваемой ИГП проводились на базе табличного процесса EXCEL. Ниже в графическом формате представлена динамика абсолютных и относительных показателей эффективности для структурных подразделений и управляющей компании.



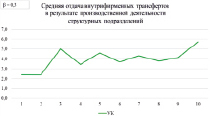
Рис. 1. Динамика абсолютных и относительных показателей эффективности для структурных подразделений и управляющей компании при β = 0,3




Рис. 2. Динамика абсолютных и относительных показателей эффективности для структурных подразделений и управляющей компании при β = 0,5
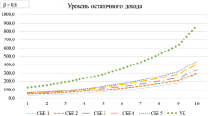



Рис. 3. Динамика абсолютных и относительных показателей эффективности для структурных подразделений и управляющей компании при β = 0,8
Убедившись в дееспособности приведенной модели, рассмотрим задачу увеличения объема централизованного инвестиционного фонда холдинга Ωt на конец временных периодов t и увеличение средней отдачи внутрифирменных трансфертов в результатах производственной деятельности структурных подразделений холдинга для выбранного уровня риска структуры их рабочих капиталов, равного β = 0,3.
Задача 1.
Провести перераспределение долей внутрифирменных трансфертов для СБЕ: 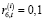 (i = 1; t =
(i = 1; t = 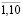 );
); 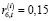 (i = 2; t =
(i = 2; t = 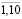 );
); 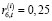 (i =
(i = 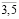 ; t =
; t = 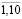 ).
).
Объем внутрифирменных трансфертов не изменился и составил 60 % от объема накопленного централизованного инвестиционного фонда холдинга: 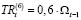 (t = 1, … ,10). Доля отчислений каждой СБЕ в централизованный инвестиционный фонд осталась без изменений (на постоянном уровне в соответствии исходными данными производственной сферы моделируемой ИГП:
(t = 1, … ,10). Доля отчислений каждой СБЕ в централизованный инвестиционный фонд осталась без изменений (на постоянном уровне в соответствии исходными данными производственной сферы моделируемой ИГП: 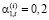 (i =
(i = 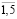 ; t =
; t = 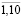 );
); 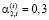 (i = 1,2; t =
(i = 1,2; t = 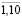 );
); 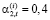 (i = 3,4,5; t =
(i = 3,4,5; t = 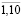 ).
).
Результаты моделирования представлены на рис. 4.
Таким образом, проведенная коррекция трансфертов позволила улучшить динамику производственной сферы менее эффективной СБЕ 1.
Для того, чтобы увеличить объем средств, направляемых в адрес управляющей компании, на первом шаге было принято решение о перечислении большего числа внутрифирменных трансфертов «лидирующим» СБЕ: 3-й, СБЕ 4-й и 5-й. Результаты представлены в табл. 2.
Задача 2.
Провести анализ динамики объема централизованного инвестиционного фонда холдинга Ωt на конец временных периодов t, обусловленной изменением нормы распределения остаточного дохода подразделениями холдинга.
Объем внутрифирменных трансфертов и доля их распределения для каждой СБЕ остался неизменным в соответствии с данными первой задачи.
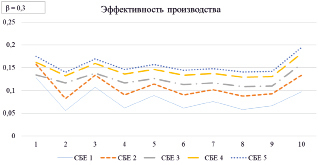
Рис. 4. Эффективность рыночной деятельности подразделений ИГП на временных интервалах t = 
Таблица 2
Показатели объема централизованного инвестиционного фонда холдинга и средней отдачи внутрифирменных трансфертов при β = 0,3
|
t = 0 |
t = 1 |
t = 2 |
t = 3 |
t = 4 |
t = 5 |
t = 6 |
t = 7 |
t = 8 |
t = 9 |
t = 10 |
|
|
Ωt |
100 |
84,8 |
81,4 |
116,1 |
136,4 |
187,0 |
227,8 |
300,5 |
370,8 |
477,6 |
798,7 |
|
эt(i) |
0,0 |
2,3 |
2,7 |
4,9 |
3,7 |
4,6 |
3,9 |
4,3 |
3,9 |
4,2 |
5,8 |
Таблица 3
Нормы распределение остаточного дохода на пополнение централизованного фонда холдинга
|
Номер СБЕ |
t = 1 |
t = 2 |
t = 3 |
t = 4 |
t = 5 |
t = 6 |
t = 7 |
t = 8 |
t = 9 |
t = 10 |
|
α (2,t) |
||||||||||
|
i = 1, 2 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
i = 3, 4, 5 |
0,5 |
0,55 |
0,6 |
0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,9 |
Поскольку приоритетной целью является увеличение объема централизованного фонда, распределение остаточного дохода каждой СБЕ удовлетворяло следующим условиям: распределение остаточного дохода на непроизводственное потребление снижено в сравнении с исходными данными и их доля составила: 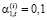 (i =
(i = 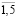 ; t =
; t = 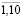 ).
).
Нормы распределение остаточного дохода на пополнение централизованного фонда холдинга для каждой i-й СБЕ представлены в таблице (табл. 3).
На рисунке 5 представлена динамика объема централизованного фонда холдинга в соответствии с проведенной коррекцией и в сравнении с исходным распределением остаточного дохода каждой i-й СБЕ, используемой в постановке первой задачи.
Исходя из графика, можно сделать вывод, что постепенное увеличение отчислений СБЕ в бюджет управляющей компании положительно влияет на объем централизованного инвестиционного фонда холдинга.
Стоит отметить, что средняя отдача внутрифирменных трансфертов в результате производственной деятельности при данной коррекции показала значительный спад в середине моделируемого периода (рисунок 6).
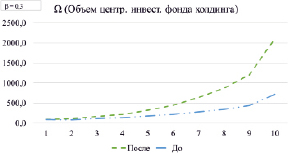
Рис. 5. Объемы централизованного инвестиционного фонда холдинга
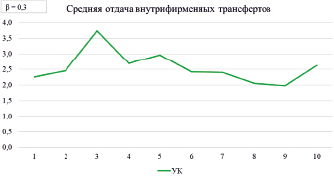
Рис. 6. Динамика средней отдачи внутрифирменных трансфертов в результатах производственной деятельности подразделений холдинга
Задача 3.
Исследована динамика наполняемости объема централизированного инвестиционного фонда и средняя отдача внутрифирменных трансфертов с позиции изменения объема отчислений, направленных на внутрифирменные трансферты.
Предполагается ситуация, при которой доля трансфертных платежей в первом периоде составляет 60 % от объема накопленного централизованного инвестиционного фонда холдинга 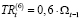 (t = 1). Каждый последующий период доля отчислений сокращается на 6 %. Значение доли трансфертных платежей для каждого периода представлены в таблице (таблица 4).
(t = 1). Каждый последующий период доля отчислений сокращается на 6 %. Значение доли трансфертных платежей для каждого периода представлены в таблице (таблица 4).
Комментарий. Параметры 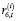 – доля внутрифирменных трансфертов для i-й СБЕ,
– доля внутрифирменных трансфертов для i-й СБЕ, 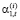 ,
, 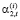 – нормы распределения остаточного дохода на непроизводственное потребление остались неизменными в соответствии с исходными данными.
– нормы распределения остаточного дохода на непроизводственное потребление остались неизменными в соответствии с исходными данными.
Таблица 4
Доля трансфертных платежей на исследуемом временном интервале
|
t = 1 |
t = 2 |
t = 3 |
t = 4 |
t = 5 |
t = 6 |
t = 7 |
t = 8 |
t = 9 |
t = 10 |
|
|
|
60 % |
54 % |
48 % |
42 % |
36 % |
30 % |
24 % |
18 % |
12 % |
6 % |
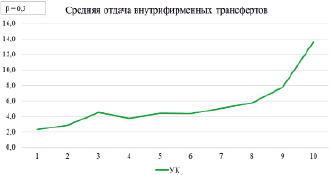
Рис. 7. Динамика средней отдачи внутрифирменных трансфертов в результате производственной деятельности
Таблица 5
Динамика объема централизованного инвестиционного фонда при β = 0,3
|
t = 0 |
t = 1 |
t = 2 |
t = 3 |
t = 4 |
t = 5 |
t = 6 |
t = 7 |
t = 8 |
t = 9 |
t = 10 |
|
|
Ωt |
100 |
98,1 |
116,6 |
189,6 |
273,0 |
423,9 |
642,1 |
1001,4 |
1544,2 |
2414,8 |
3699,9 |
Данная коррекция позволила увеличить среднюю отдачу от внутрифирменных трансфертов (рисунок 7).
В процессе сокращения доли внутрифирменных отчислений наблюдался значительный прирост объема централизованного инвестиционного фонда. Результаты расчета средств, наколенных на конец каждого из периодов, представлены в таблице (таблица 5).
Результаты расчетов динамики внутрифирменных денежных потоков холдинга
Значительное увеличение объема централизованного инвестиционного фонда холдинга наблюдалось при изменении параметров:
– остаточный доход подразделений – СБЕ;
– объемы внутрифирменных трансфертов.
Постепенное сокращение внутрифирменных трансфертов введет к накоплению остатка средств централизованного инвестиционного фонда. Дополнительным значимым фактором, положительно влияющим на темп роста объема средств управляющей компании, является повышение доли отчислений остаточного дохода каждой СБЕ на пополнение централизованного фонда холдинга.
Стоит отметить, что для СБЕ с высокой эффективностью производственной сферы рекомендуется направлять большие объемы внутрифирменных трансфертов. В нашем случае, «лидирующими» предприятиями являются третье, четвертое и пятое СБЕ. Как показал анализ, такое решение положительно сказывается на объёме средств, перечисляемых в адрес управляющей компании.
Задача 4.
Провести расчеты средневзвешенной стоимости рабочих капиталов СБЕ холдинга и оценить стоимость генерируемых денежных потоков.
Для оценки NPV (31) был рассчитан показатель средневзвешенной стоимости капитала (32) по балансу за 2019 г. холдинга «Вертолеты России» представленный в таблице (таблица 6).
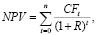 (1)
(1)
где CF – денежный поток (Cash Flow); R – средневзвешенная стоимость капитала.
R = kdwd (1 – T) + kewe, (2)
где kd – средняя стоимость заемного капитала компании; wd – удельный вес заемного капитала в структуре рабочего капитала компании; T – ставка налога на прибыль; ke – средняя стоимость собственного капитала компании; we – удельный вес собственного капитала в структуре капитала компании.
Динамика показателя NPV для моделей, исследованных в задачах 1-3, представлена на рис. 7.
Аналогичные расчеты средневзвешенной цены капитала и стоимости денежных потоков подразделений холдинга были проведены для значений риска структуры капитала β = 0,5 и β = 0,8. Результаты представлены в табл. 8, 9 и на рис. 9.
Таблица 6
Расчет WACC холдинга при β = 0,3
|
Показатели |
Значения |
Инфо. |
|
Стоимость собственного капитала |
13,67 % |
ke |
|
Чистая прибыль |
13 157 559 |
руб. |
|
Собственный капитал |
96 266 182 |
руб. |
|
Стоимость заемного капитала |
4,19 % |
kd |
|
Проценты к уплате |
2 582 895 |
руб. |
|
Заемный капитал |
61 649 349 |
руб. |
|
Процентная ставка налога на прибыль (t) |
20 % |
T |
|
Вес акционерного (собственного) капитала |
61 % |
we |
|
Вес заемного капитала |
39 % |
wd |
|
WACC |
9,64 % |
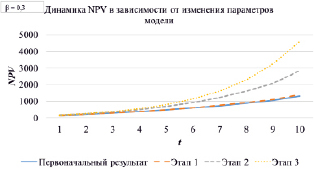
Рис. 8. Динамика NPV для моделей задач 1-3 и для случая β = 0,3
Таблица 7
Показатели объема централизованного инвестиционного фонда холдинга и средней отдачи внутрифирменных трансфертов при β = 0,3
|
Первоначальный результат |
||||||||||||
|
t = 0 |
t = 1 |
t = 2 |
t = 3 |
t = 4 |
t = 5 |
t = 6 |
t = 7 |
t = 8 |
t = 9 |
t = 10 |
NPV |
|
|
Ωt |
100 |
89,3 |
78,7 |
115,6 |
130,5 |
180,5 |
214,7 |
283,5 |
343,7 |
441,7 |
720,9 |
1256,0 |
|
эt(i) |
0,0 |
2,4 |
2,4 |
5,0 |
3,4 |
4,6 |
3,7 |
4,3 |
3,8 |
4,1 |
5,7 |
|
|
Окончание табл. 7 |
||||||||||||
|
Этап 1 |
||||||||||||
|
t = 0 |
t = 1 |
t = 2 |
t = 3 |
t = 4 |
t = 5 |
t = 6 |
t = 7 |
t = 8 |
t = 9 |
t = 10 |
NPV |
|
|
Ωt |
100 |
84,8 |
81,4 |
116,1 |
136,4 |
187,0 |
227,8 |
300,5 |
370,8 |
477,6 |
798,7 |
1338,9 |
|
эt(i) |
0,0 |
2,3 |
2,7 |
4,9 |
3,7 |
4,6 |
3,9 |
4,3 |
3,9 |
4,2 |
5,8 |
|
|
Этап 2 |
||||||||||||
|
t = 0 |
t = 1 |
t = 2 |
t = 3 |
t = 4 |
t = 5 |
t = 6 |
t = 7 |
t = 8 |
t = 9 |
t = 10 |
NPV |
|
|
Ωt |
100 |
96,9 |
106,8 |
167,5 |
220,0 |
324,4 |
443,8 |
638,4 |
866,5 |
1200,5 |
2108,2 |
2931,1 |
|
эt(i) |
0,0 |
2,3 |
2,5 |
3,7 |
2,7 |
3,0 |
2,4 |
2,4 |
2,1 |
2,0 |
2,6 |
|
|
Этап 3 |
||||||||||||
|
t = 0 |
t = 1 |
t = 2 |
t = 3 |
t = 4 |
t = 5 |
t = 6 |
t = 7 |
t = 8 |
t = 9 |
t = 10 |
NPV |
|
|
Ωt |
100 |
98,1 |
116,6 |
189,6 |
273,0 |
423,9 |
642,1 |
1001,4 |
1544,2 |
2414,8 |
3699,9 |
4850,4 |
|
эt(i) |
0,0 |
2,3 |
2,9 |
4,5 |
3,8 |
4,4 |
4,4 |
5,0 |
5,7 |
7,8 |
13,6 |
|
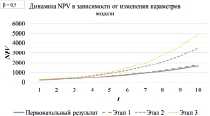
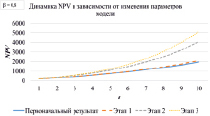
Рис. 9. Динамика NPV в зависимости от изменения параметров модели для β = 0,5 и β = 0,8
Таблица 8
Показатели объема централизованного инвестиционного фонда холдинга и средней отдачи внутрифирменных трансфертов для β = 0,5
|
Первоначальный результат |
||||||||||||
|
t = 0 |
t = 1 |
t = 2 |
t = 3 |
t = 4 |
t = 5 |
t = 6 |
t = 7 |
t = 8 |
t = 9 |
t = 10 |
NPV |
|
|
Ωt |
100 |
111,7 |
115,8 |
148,8 |
183,8 |
230,8 |
287,2 |
356,8 |
441,5 |
544,5 |
806,4 |
1607,3 |
|
эt(i) |
0,0 |
3,5 |
3,1 |
4,2 |
4,0 |
4,1 |
4,0 |
4,0 |
4,0 |
4,0 |
5,1 |
|
|
Задача 1 |
||||||||||||
|
t = 0 |
t = 1 |
t = 2 |
t = 3 |
t = 4 |
t = 5 |
t = 6 |
t = 7 |
t = 8 |
t = 9 |
t = 10 |
NPV |
|
|
Ωt |
100 |
111,8 |
117,7 |
153,5 |
192,0 |
244,1 |
307,3 |
386,2 |
483,2 |
602,5 |
906,7 |
1738,6 |
|
эt(i) |
0,0 |
3,5 |
3,2 |
4,3 |
4,1 |
4,1 |
4,1 |
4,1 |
4,0 |
4,0 |
5,1 |
|
|
Задача 2 |
||||||||||||
|
t = 0 |
t = 1 |
t = 2 |
t = 3 |
t = 4 |
t = 5 |
t = 6 |
t = 7 |
t = 8 |
t = 9 |
t = 10 |
NPV |
|
|
Ωt |
100 |
131,0 |
154,5 |
222,1 |
304,0 |
418,9 |
582,9 |
806,1 |
1100,2 |
1486,5 |
2333,8 |
3656,0 |
|
эt(i) |
0,0 |
3,5 |
2,7 |
3,3 |
2,9 |
2,7 |
2,5 |
2,3 |
2,1 |
1,9 |
2,3 |
|
|
Задача 3 |
||||||||||||
|
t = 0 |
t = 1 |
t = 2 |
t = 3 |
t = 4 |
t = 5 |
t = 6 |
t = 7 |
t = 8 |
t = 9 |
t = 10 |
NPV |
|
|
Ωt |
100 |
132,2 |
165,0 |
247,7 |
359,7 |
524,5 |
774,0 |
1142,2 |
1674,0 |
2438,7 |
3447,8 |
5211,3 |
|
эt(i) |
0,0 |
3,5 |
3,1 |
4,0 |
3,9 |
4,0 |
4,2 |
4,6 |
5,3 |
6,8 |
11,4 |
|
Таблица 9
Показатели объема централизованного инвестиционного фонда холдинга и средней отдачи внутрифирменных трансфертов для β = 0,8
|
Первоначальный результат |
||||||||||||
|
t = 0 |
t = 1 |
t = 2 |
t = 3 |
t = 4 |
t = 5 |
t = 6 |
t = 7 |
t = 8 |
t=9 |
t=10 |
NPV |
|
|
Ωt |
100 |
129,7 |
154,4 |
190,1 |
234,0 |
287,5 |
352,0 |
429,7 |
523,0 |
634,8 |
867,0 |
1935,7 |
|
эt(i) |
0,0 |
4,3 |
3,8 |
4,0 |
4,0 |
4,0 |
4,0 |
4,0 |
4,0 |
4,0 |
4,7 |
|
|
Задача 1 |
||||||||||||
|
t = 0 |
t = 1 |
t = 2 |
t = 3 |
t = 4 |
t = 5 |
t = 6 |
t = 7 |
t = 8 |
t=9 |
t=10 |
NPV |
|
|
Ωt |
100 |
130,4 |
157,3 |
196,3 |
245,0 |
305,0 |
378,3 |
467,8 |
576,4 |
708,2 |
981,8 |
2100,7 |
|
эt(i) |
0,0 |
4,4 |
3,9 |
4,1 |
4,1 |
4,0 |
4,0 |
4,0 |
4,0 |
3,9 |
4,6 |
|
|
Задача 2 |
||||||||||||
|
t = 0 |
t = 1 |
t = 2 |
t = 3 |
t = 4 |
t = 5 |
t = 6 |
t = 7 |
t = 8 |
t=9 |
t=10 |
NPV |
|
|
Ωt |
100 |
155,0 |
207,6 |
283,6 |
384,2 |
515,5 |
704,9 |
957,8 |
1287,1 |
1711,1 |
2474,0 |
4278,5 |
|
эt(i) |
0,0 |
4,3 |
3,3 |
3,1 |
2,9 |
2,7 |
2,5 |
2,3 |
2,1 |
1,9 |
2,0 |
|
|
Задача 3 |
||||||||||||
|
t = 0 |
t = 1 |
t = 2 |
t = 3 |
t = 4 |
t = 5 |
t = 6 |
t = 7 |
t = 8 |
t=9 |
t=10 |
NPV |
|
|
Ωt |
100 |
156,0 |
217,4 |
310,3 |
439,5 |
616,3 |
875,8 |
1237,0 |
1725,8 |
2372,5 |
3146,5 |
5421,5 |
|
эt(i) |
0,0 |
4,3 |
3,7 |
3,8 |
3,8 |
3,8 |
4,0 |
4,3 |
4,8 |
6,0 |
9,8 |
|
Вывод
Результаты расчетов стоимости денежных потоков наглядно демонстрируют отмеченный в более ранней работе авторов факт роста эффективности и стоимости компании (в данном случае, производственного холдинга) с ростом доли заемного финансирования в рабочем капитале. Однако, при этом растет и риск банкротства.
Библиографическая ссылка
Димитриев А.М., Москвичев К.В. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ВНУТРИФИРМЕННЫХ ДЕНЕЖНЫХ ПОТОКОВ ИНТЕГРИРОВАННОЙ ПРОИЗВОДСТВЕННОЙ СТРУКТУРЫ (ПРОДОЛЖЕНИЕ) // Вестник Алтайской академии экономики и права. 2020. № 5-1. С. 53-64;URL: https://vaael.ru/ru/article/view?id=1112 (дата обращения: 11.03.2026).
DOI: https://doi.org/10.17513/vaael.1112