Научный журнал

Вестник Алтайской академии экономики и права

Print ISSN 1818-4057

Online ISSN 2226-3977

Перечень ВАК

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ильина Е.А. 1 Парфенова А.Ю. 1 Сараев Л.А. 1

---

1 ФГАОУ ВО «Самарский национальный исследовательский университет им. академика С.П. Королева»

В публикуемой статье предложена математическая модель диффузии потребительских инноваций, учитывающая изменение во времени общего числа потенциальных покупателей. Исследование особенностей и закономерностей процессов распространения на рынках товаров с новыми свойствами представляет собой актуальную проблему современной экономической теории. Разработка новых математических моделей, описывающих процессы диффузии потребительских инноваций, помогает адекватно оценивать скорости роста продаж товаров с новыми свойствами, прогнозировать показатели захвата ими рынков, рассчитывать временные интервалы стагнации или снижения их продаж и т. д. Целью публикуемой работы является разработка новой экономико-математической модели диффузии инноваций в условиях нестабильного поведения потребителей. Эта модель представляет собой нелинейное дифференциальное уравнение переменными коэффициентами. Особенность предлагаемой модели и ее научная новизна заключается в том, что она в отличие от классической модели диффузии инноваций учитывает изменение во времени общего числа потенциальных покупателей, числа покупателей-новаторов, и числа покупателей-имитаторов. Кроме того, модель способна описывать различные варианты заполнения рынка инновационным товаром. К таким вариантам относятся монотонный процесс диффузии инноваций, процессы временной стагнации или временного падения продаж. Построены уравнение изменения общего числа участников рынка и уравнение роста покупателей инновационного товара. Рассмотрены три ситуации развития процесса диффузии инноваций. Для первой ситуации инновации распространяются стабильно и поступательно. Для второй ситуации процесс диффузии инноваций приостанавливается на некотором временном интервале. Для третьей ситуации процесс диффузии инноваций характеризуется определенным сворачиванием на некотором временном интервале. Численный анализ разработанной модели показал хорошее соответствие известным статистическим данным роста числа пользователей глобальной сети интернет в России.

Статья в формате PDF

0 KB

инновация

диффузия инноваций

коэффициент инновации

коэффициент имитации

1. Bass F.M. A new product growth model for consumer durables // Management Science. 1969. vol. 15. P. 215–227.

2. Сараев А.Л. Влияние производственных издержек предприятия на динамику его прибыли // Вестник Самарского государственного университета. 2015. № 9 (131). С. 293–298.

3. Исследование GfK: проникновение интернета в России [Электронный ресурс]. URL: https://www.gfk.com/fileadmin/user_upload/dyna_content/RU/Documents/Press_Releases/ 2019/GfK_Rus_Internet_Audience_in_Russia_2018.pdf (дата обращения: 14.11.2019).

Введение

Исследование особенностей и закономерностей процессов распространения на рынках товаров с новыми свойствами представляет собой актуальную проблему современной экономической теории.

Разработка новых математических моделей, описывающих процессы диффузии потребительских инноваций, помогает адекватно оценивать скорости роста продаж товаров с новыми свойствами, прогнозировать показатели захвата ими рынков, рассчитывать временные интервалы стагнации или снижения их продаж и т. д.

Целью публикуемой работы является разработка новой экономико-математической модели диффузии инноваций в условиях нестабильного поведения потребителей. Эта модель представляет собой нелинейное дифференциальное уравнение переменными коэффициентами.

Особенность предлагаемой модели и ее научная новизна заключается в том, что она в отличие от классической модели диффузии инноваций учитывает изменение во времени общего числа потенциальных покупателей, числа покупателей-новаторов, и числа покупателей-имитаторов. Кроме того, модель способна описывать различные варианты заполнения рынка инновационным товаром.

К таким вариантам относятся монотонный процесс диффузии инноваций, процессы временной стагнации или временного падения продаж.

Модель процесса диффузии инноваций, учитывающая изменения общего числа потенциальных покупателей

Пусть на рынке появляется и распространяется принципиально новый инновационный товар. Обозначим U = U(t) – число покупателей этого товара в момент времени t.

Функция U = U(t) непрерывного аргумента t считается непрерывной и непрерывно дифференцируемой на интервале (0 ≤ t ≤ ∞).

Приращение числа покупателей инновационного товара ΔU за некоторый промежуток времени Δt можно представить в виде двух слагаемых

ΔU = ΔU^N + ΔU^I. (1)

Здесь ΔU^N – частичное приращение за промежуток времени Δt числа покупателей-новаторов, ориентирующихся на рекламу и средства массовой информации, ΔU^I – частичное приращение за промежуток времени Δt числа покупателей-имитаторов, полагающихся на отзывы уже совершивших приобретение людей. Величины ΔU^N, ΔU^I можно представить в виде

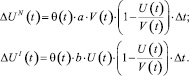(2)

Здесь a – коэффициент инновации, определяющий долю покупателей-новаторов от общего числа потенциальных покупателей V(t); b – коэффициент имитации, определяющий долю покупателей-имитаторов от числа покупателей уже совершивших покупку U(t), θ(t) – функция, описывающая относительную скорость поступления на рынок инновационного товара.

Множитель 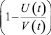– описывает процесс насыщения рынка до некоторого предельного значения V(t). Следует отметить, что в рассматриваемой модели в отличие от классической модели Ф. Басса общее число потенциальных покупателей V(t) не является константой, а предполагается переменной величиной [1].

Подставляя соотношения (2) в формулу (1), находим

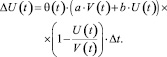(3)

Переходя в соотношении (3) к пределу при Δt → 0, находим нелинейное дифференциальное уравнение

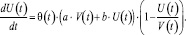(4)

Начальное условие для уравнения (4) имеет вид

U(0) = U₀. (5)

Очевидно, что если процесс диффузии инноваций наблюдается с самого начала, то U₀ = 0. В противном случае значение U0 может отличаться от нуля.

В общем случае нелинейная задача Коши (4), (5) с переменным коэффициентом V(t) может быть решена только численно.

Рассмотрим вариант развития продвижения на рынок инновационного товара, при котором в начальный момент времени t наибольшее число его потенциальных покупателей составляет V₀, а затем это число постепенно изменяется до определенного предела V_∞.

Предположим, что изменение числа покупателей ΔV(t) за время Δt будет пропорционально отклонению функции P(t) от предельного значения V_∞

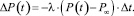(6)

Переход к пределу при условии Δt → 0 приводит к дифференциальному уравнению для функции V(t)

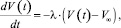(7)

решение которого с начальным условием V(0) = V0 дает

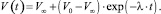(8)

Здесь λ – параметр, характеризующий скорость изменения общего числа потенциальных покупателей инновационного товара.

Формы интегральных кривых уравнения (4) будут существенно зависеть от особенностей функции относительной скорости поступления на рынок инновационного товара θ(t).

Интегральные кривые уравнений (4) будут описывать монотонный процесс заполнения рынка инновационным товаром для близких к единице значений функции θ(t), а для близких к нулю и для отрицательных значений функции θ(t) они будут описывать процессы стагнации и падения продаж инновационного товара, соответственно.

Процессы монотонного заполнения рынка, стагнации и падения продаж в окрестности некоторого момента времени t = t* удобно описывать функцией вида [2]

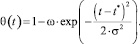(9)

Здесь ω – максимальное отклонение функции θ(t) от единицы; σ – радиус временного интервала снижения продаж.

Если параметр ω = 0, то рынок будет заполняться инновационным товаром монотонно, если параметр ω = 1, то в момент времени t = рост функции U(t) прекращается, и на интервале времени (t* – σ, t* + σ) распространение инновационного товара приостанавливается, если параметр ω > 1, то на интервале времени (t* – σ, t* + σ) продажи падают.

Если эффекты стагнации и падения продаж на рынке происходят неоднократно, то в качестве функции относительной удельной скорости поступления на рынок инновационного товара целесообразно выбрать произведение функций вида (9)

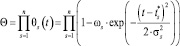(10)

На рис. 1 приведены три варианта графиков функции U(t), построенных по результатам численного решения задачи Коши (4), (5), для монотонного процесса заполнения рынка инновационным товаром, при котором параметр ω = 0.

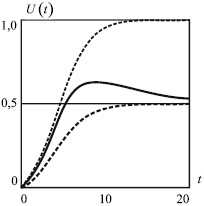
Рис. 1. Сплошная интегральная кривая функции U(t) соответствует плавному снижению емкости рынка от значения V0 до значения V_∞ . Верхняя штриховая линия кривой функции U(t) соответствует максимальной неизменяемой емкости рынка V(t) ≡ V0. Нижняя штриховая линия кривой функции U(t) соответствует минимальной неизменяемой емкости рынка V(t) ≡ V_∞ . Расчетные значения величин: V0 = 1; V_∞ = 0,5; U₀ = 0; λ = 0,2; a = 0,05; b = 0,65; ω = 0

На рис. 2 приведены три варианта графиков функции U(t), построенных по результатам численного решения задачи Коши (4), (5), для процесса заполнения рынка инновационным товаром в условиях стагнации продаж, при котором параметр ω = 1. Центр окрестности стагнации расположен в точке t* = 7,5, радиус этой окрестности составляет σ = 1,5.

На рис. 3 приведены три варианта графиков функции U(t), построенных по результатам численного решения задачи Коши (4), (5), для процесса заполнения рынка инновационным товаром в условиях падения продаж, при котором параметр ω = 1,5. Центр окрестности падения продаж расположен в точке t* = 7,5, радиус этой окрестности составляет σ = 1,5.

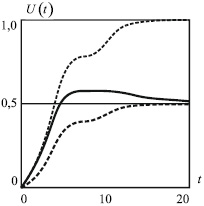
Рис. 2. Сплошная интегральная кривая функции U(t) соответствует плавному снижению емкости рынка от значения V0 до значения V∞. Верхняя штриховая линия кривой функции U(t) соответствует максимальной неизменяемой емкости рынка V(t) ≡ V0. Нижняя штриховая линия кривой функции U(t) соответствует минимальной неизменяемой емкости рынка V(t) ≡ V∞. Расчетные значения величин: V0 = 1; V∞ = 0,5; U0 = 0; λ = 0,2; a = 0,05; b = 0,65; ω = 1; t* = 7,5; σ = 1,5

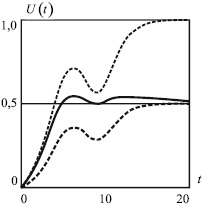
Рис. 3. Сплошная интегральная кривая функции U(t) соответствует плавному снижению емкости рынка от значения V0 до значения V∞. Верхняя штриховая линия кривой функции U(t) соответствует максимальной неизменяемой емкости рынка V(t) ≡ V0. Нижняя штриховая линия кривой функции U(t) соответствует минимальной неизменяемой емкости рынка V(t) ≡ V∞. Расчетные значения величин: V0 = 1; V∞ = 0,5; U0 = 0; λ = 0,2; a = 0,05; b = 0,65; ω = 1,5; t* = 7,5; σ = 1,5

Если в рассматриваемой модели общее число потенциальных покупателей принять постоянной величиной V(t) = const, то построенная модель продвижения на рынок инновационного товара будет совпадать с известной моделью Ф. Басса [1].

Применим теперь построенную модель для расчета показателей роста числа пользователей глобальной сети интернет в России, общая аудитория которых по данным Всероссийского омнибуса GfK к началу 2019 года составила 75,4 % взрослого населения страны. Статистические данные относительного роста интернет-пользователей приведены в табл. 1 [3].

Таблица 1

В соответствии с данными табл. 1, уравнение (4) с функцией (10) и начальным условием (5) принимают вид

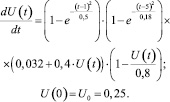(11)

На рис. 4 приведено сравнение графика функции роста числа пользователей интернет U(t), построенного по результатам численного решения задачи Коши (11) и наблюдаемых данных, построенных по табл. 1.

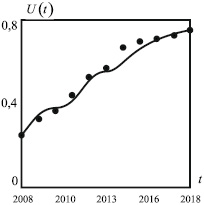
Рис. 4. Интегральная кривая функции U(t) представляет собой численное решение задачи Коши (11). Точками обозначены наблюдаемые значения функции U(t), построенные по данным табл. 1. Расчетные значения параметров: V0 = 0,8; V∞ = 0,8; U0 = 0,25; λ = 0,15; a = 0,04; b = 0,4

Следует отметить, что в соответствии с данными табл. 1 в 2010 году (ω = 1; σ = 0,5) и в 2013 году (ω = 1; σ = 0,3) наблюдалась определенная стагнация распространения числа пользователей интернет.

Основной тенденцией последних лет является рост пользователей сети интернет, использующих мобильные устройства, главную часть аудитории пользователей составляют владельцы смартфонов. Статистические данные относительного роста мобильных интернет-пользователей приведены в табл. 2 [3].

Таблица 2

Применим построенную модель для расчета показателей роста числа владельцев смартфонов к данным табл. 2. В соответствии с данными табл. 2, уравнение (4) с функцией (10) и начальным условием (5) принимают вид

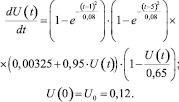(12)

На рис. 5 приведено сравнение графика функции роста числа владельцев смартфонов U(t), построенного по результатам численного решения задачи Коши (12) и наблюдаемых данных, построенных по табл. 2.

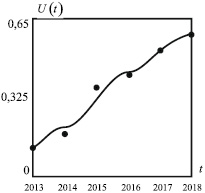
Рис. 5. Интегральная кривая функции U(t) представляет собой численное решение задачи Коши (12). Точками обозначены наблюдаемые значения функции U(t), построенные по данным табл. 2. Расчетные значения параметров: V0 = 0,65; V∞ = 0,65; U0 = 0,12; λ = 0,75; a = 0,05; b = 0,95

Следует отметить, что в соответствии с данными табл. 2 в 2014 году (ω = 1; σ = 0,2) и в 2016 году (ω = 1; σ = 0,2) наблюдалась определенная стагнация распространения числа пользователей смартфонами.

Другой тенденцией последних лет является сокращение с определенного момента использования планшетов частью аудитории пользователей интернет. Статистические данные такого изменения относительного числа интернет-пользователей с помощью планшетов приведены в табл. 3 [3].

Таблица 3

Применим построенную модель для расчета показателей изменения числа владельцев планшетов к данным табл. 3. В соответствии с данными табл. 3, уравнение (4) с начальным условием (5) принимают вид

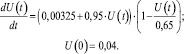(13)

На рис. 6 приведено сравнение графика функции роста числа мобильных пользователей интернет U(t), построенного по результатам численного решения задачи Коши (13) и наблюдаемых данных, построенных по табл. 3.

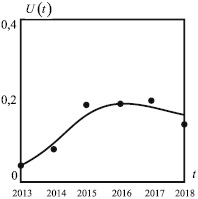
Рис. 6. Интегральная кривая функции U(t) представляет собой численное решение задачи Коши (12). Точками обозначены наблюдаемые значения функции U(t), построенные по данным табл. 2. Расчетные значения параметров: V0 = 0,65; V∞ = 0,65; U0 = 0,12; λ = 0,75; a = 0,05; b = 0,95

Заключение

Разработана новая модель диффузии инноваций, учитывающая изменение во времени общего числа потенциальных приобретателей. Исследовано влияние изменения числе потенциальных покупателей на процесс диффузии инноваций.

Рассмотрены три варианта процесса диффузии инноваций. В первом случае инновации распространяются стабильно и поступательно. Во втором случае процесс диффузии инноваций временно приостанавливается. В третьем случае процесс диффузии инноваций временно сворачивается.

Численный анализ разработанной модели показал хорошее соответствие известным статистическим данным роста числа пользователей глобальной сети интернет в России.

Библиографическая ссылка